00098471

234

i na odwrót, każdej liczbie zespolonej (111.4) jest przyporządkowany dokładnie jeden punkt P(x;y) płaizczyzny. Utożsamiając punkty P(x;y) rozważanej płaszczyzny z liczba nu z = x+Jy mówimy, że jest to płaszczyzna liczbowa albo płaszczyzna zespolona (dokładniej: płaszczyzna zespolona otwarta); płaszczyzną tą oznaczać będziemy symbolem Z.

234

y

(W) Z

Rw. ra.i

Odległość punktu z od punktu 0 (rys. IIU) nazywamy modułem liczby zespolonej z i oznaczamy symbolem |z|. Mamy więc

(m.5)

nazywamy orgi

liczby zespolonej. Oczywiście, każda liczba zespolona (różna

od zera) ma nieskończenie wiele argumentów. Każcie dwa spośród nich różnią się między sobą o całkowitą wielokrotność liczby 2rc. Ten z argumentów, który należy do przedziału (—n, +w) nazywamy argumentem głównym i oznaczamy symbolem argz albo literą ?■ Argument główny jest określony jednoznacznie, co wynika z po* stad warunków (III. 5).

Zbiór wszystkich argumentów liczby zespolonej z + 0 oznaczamy symbolem Argr i nazywamy argumentem -wieloznacznym (krótko: argumentem). Elementy tego zbioru nazywamy wartoiciam argumentu wieloznacznego Piszemy przy tym

łub krótko

Afgz-argjr+2ir* (k » 0, ± 1, ±2,,..)

i - p+2ffk

mąjąc na myśli. Że do zbioru Argz należą wszytlue te i tylko te liczby, które różnią się od argz o całkowitą wielokrotność 2*.

Zwracamy uaan. te symbol Arg z oznaem nie Jadną liczbą tocs iMtu nteslrcteawiie wielu

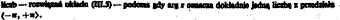
Argz .można interpretować jako zbiór wszystkich miar lukowych kąta skierowanego wektora OP (rył. ULI) z osią rzeczywistą. Argument główny <p stanowi tę miarę łukową tego kąta, która należy do przedziału (—w, ze>.

Uwaga. Odnośnie argumentu liczby zespolonej 0 można zajmować jedno z dfcóch ttano-wilk: argument liczby 0 nie Jest okrtilony albo (stanowisko bardziej wygodne) kaida liczba rzeczywista jest argumentem liczby 0. W tym drugim przypadku każdą liczbę z przedziału (— rt. + *> można uwalać a argument główny liczby 0.

Pamiętamy, że każdą liczbę zespoloną (Iil.4) można zapisać w postaci trygonometrycznej

z - ]z| (cos 4+./sin 4)    (in.6)

We wzorze tym można podBtawić na miejsce <f> jakąkolwiek wartość Arg z, na przykład argument główny.

Symbol |z[ modułu liczby z zastępujemy często jedną Hterą, na przykład r albo ę.

Jeżeli z, i z_a są dwiema różnymi od zera liczbami zespolonymi, to prawdziwe są następujące zależności:

moduł iloczynu równa się iloczynowi modułów

moduł ilorazu równa się ił orazowi modułów

I *i 1 I »t I •

| *a I ~ I *a |

argument iloczynu równa się sumie argumentów

Arg(a, • *,) - Arg a, -f Arg a_a    m 7)

argument ilorazu równa się różnicy argumentów

Arg-^L = Arg z, — Arg a,    OILS)

*2

Uwaga 1. Równość (H17) oaaaaa, że dla każdej wartości tfc, argumentu Arg (a,• a») kuleje taka wartość 4>i ar^aneota Arg a, onu fatnłeje taka wartość fa argumentu Arg u. te — fi+jt- Równość (Tfl.ł) należy rraunńeć analogicznie.

Uwaga 2. JażaB we wzorach fln.7) I (HM) laitąpiaij aymbołe argumentu (Arg) tym-bolami arpanezsów głównych (wg), to otrzymamy równości fthtywe. Irtotsh, przyjmując na pnytM a, - -I, *»-i. temny

Wtfi. »i)r-j-. argz, - *g(-l) ~ +*,

*»*a - arg/- +-J

nfgłi./J^afgr.+arił,