00098472

236 I. fTJNKCJE ZMIENNEJ ZESPOLONEJ

Podobnie, przyjmując t, -    d im łajemy

ar* ii. - ar*( I)- ł «.

^ar* *> ■‘Itł - ^ ₂

a więc

ar* —»i ar*r, -ar*r,

Z uwagi na postać trygonometryczną (111.6) liczby zespolonej oraz ze względu na niezwykle ważny w zastosowaniach wzór Eulera

e¹* ■■=■ cos a +j sin a

(a oznacza to dowolną liczbę rzeczywistą) każdą liczbę zespoloną można zapisać w tzw. postaci wykładniczej

z - re>*    (Itl-9)

W powyższym wzorze r oznacza moduł, f — argument liczby zespolonej i W dalszym ciągu będziemy C2ęsto korzystać ze wzoru Mororea (cos a+jsin a)* — cos«a ¹ /sin aa

w którym a oznacza dowolną liczbę rzeczywistą, n zaś dowolną liczbę naturalną Na zakończenie przypominamy pierwiastkowanie liczb zespolonych. Jeżeli 2 — r(cosę^l-r/sinę>), gdzie rp = argz, to

y; - \r< (co*    +;»„na.oi

(k = 0,1,2,... it—I)

Jeżeli z »» 0, to pierwiastek '/I ma dokładnie n różnych wartości. Podstawiając we wzorze (Ul. 10) A = 0, dostajemy tzw. pierwiastek główny stopnia n z liczby t, który oznaczony symbolem |£~?: mamy więc

if7 - V'    +/"»•[)

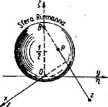
Po tym krótkim przeglądzie podstawowych określeń i wzorów z zakresu algebry liczb zespolonych, powracamy do pojęcia płaszczyzny liczbowej, którą nazwaliśmy także płaszczyzną zespoloną otwartą. Rozważmy zatem taką właśnie płaszczyznę Z oraz wyobraźmy sobie kulę o jednostkowej średnicy, styczną do tej płaszczyzny w początku układu Osty (rys. III.2). Powierzchnię tej kuli nazywamy sferą Riemanna. Punkt O, czyli punkt styczności sfery Riemanna z płaszczyzną liczbową, nazywamy biegunem południowym, zaś punkt B — położony na tej sferze i przeciwległy punktowi

0    — nazywamy biegunem północnym.

Bierzemy pod uwagę dowolny punkt r położony na płaszczyźnie liczbowej

1    łączymy go odcinkiem z biegunem północnym B. Niech P + B oznacza ten punkt

rozważanego odcinka, który leży na sferze Riemanna. W laki sposób można każdemu punktowi z Jeżącemu na płaszczyźnie otwartej Z przyporządkować (wzajemnie jednoznacznie) punkt P leżący na sferze Riemanna. Przyporządkowanie talde nazywa się rzutem stereogrttficznym. Zauważmy, że punkt B, jako jedyny z całej

■?

Rvs. m.2

sfery Riemanna, nie jest przyporządkowany w rzucie stereograficznym żadnemu punktowi płaszczyzny liczbowej, W związku z tym uzupełniamy płaszczyznę zespoloną otwartą Z tzw. punktem w nieskończoności, który oznaczamy symbolem oo. Za obraz punktu z = co w rzucie stereograficznym przyjmujemy z definicji punkt B, a więc środek rzutowania.

Del Płaszczyzna zespolona domknięta jest to zbiór utworzony ze wszystkich punktów płaszczyzny zespolonej otwartej oraz z punktu co.

Płaszczyznę zespoloną domkniętą nazywamy także płaszczyzną Gaussa, gdyż on właśnie wprowadził to pojęcie w 1832 r.

Rzut stereograficzny przyporządkowuje zatem wzajemnie jednoznacznie- punktom płaszczyzny Gaussa punkty sfery Riemanna.

Punkt z = oo jest punktem wewnętrznym płaszczyzny Gaussa. Przez otoczenie tego punktu rozumiemy przy tym zewnętrze każdego okręgu położonego na płaszczyźnie liczbowej, o środku w punkcie O.

ĆWICZENIA

1. Co to jat: a) liczba zwpotooa, b) jednostka urojona, c) część rzeczywista lx, U) cześć urojona Ijł, e) płaszczyzna zmpolona (czwarta), f) moduł 1.ł. ą) arjuroent lx, h) arfumeut tłówny 1-Ł?

Z Omówić postać: a) kanoniczną, b) trygonometryczną, c) wykładniczą lx Podać in-

3. Co to Jot: a) mit Hcfeom&zny, b) punkt w nieskończoności, e) płaszczyzna za-polooa domknięta?