00098498

rze D, to w jego obrazie — obszarze D' —jest określona funkcja odwrotna z =*g(^w) * która jest także holomorficzna i jednokrotna w obszarze D’, przy czym (por. wzór (111.47)).

(tn.87)

(OL88)

Dowody tych właściwości funkcji jednokrotnych pominiemy, funkcje

Wykażemy, że funkcja w jest jednokrotna w obszarze

D:    —03 <Rez< -f co,    —it<Imz<+it

Istotnie, równość tfi = e*z jest równoważna równości e*'^-*» = l,Ut kolei jest równoważną równości x,-z, = ZitkJ, i- O, ±1, ±2,... (por. rówroważnoić (W .79)), która z uwagi na drugi. z warunków (III.88) nie może być spełniona gdy z, yt tj, a to właśnie świadczy o jednokrotnośeł-runkcji (m.87) w obszarze (IU.88). Funkcja (111.87) jest holomorficzna I jednokrotna w ohsn (111.88), wi(c przekształca go na pewien obszar O'.

W celu znalezienia tego obszaru D’, przeprowadzimy następujące rozumowanie. Zapi* równość (Ul,87) w ten sposób

|w| e/“'s» >* e’eś*

przy czym z = x+jy. Ponieważ re D.wiec —ir <y < +«, a zatem

Biorąc pod uwagę zmienność x = Rez iy «= Imr, wynikającą z określenia (111-88) obszaru D, łs zauważyć, że

0<W< oo oraz -tt< argtr <+te

Obrazem O' obszaru D jest wiec cala płaszczyzna liczbowa bez ujemnej półosi (do której zal my 0). Rys. IH.I8 przedstawia interpretacje geometryczną tego przykładu.

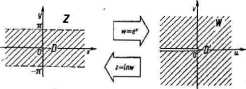
Zwróćmy uwagą, że funkcją odwrotną wzglądem (III.ST) w obalane (UL88) jest i»l«» (logarytm główny). Zgodnie z tym co powiedzieliśmy wyżej, funkcja z ^ In w jeat holomorficzna i jednokrotna w obszarze O", przy czym

wgD',

Uwaga. Funkcja (111.87) jesl oczywiście jednokrotna w każdyin obszarze, który zawiera się w pasie nieskończonym (10.88), a także w każdym pasie

—oo c Rez < +co, fldmzCó

jeżeli 0 < b-a < 2it. Na przykład Ula a = rr, 6 = 3n obrazem obszaru — pasa w przekształceniu (111.87) będzie, tak jak poprzednio, obszar D' z rys. III-18, jednakże funkcją odwrotną będzie tu nie z = Inw, lecz z — lnw j-2tr/.

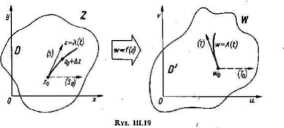
Niech /(z) będzie funkcją holomorficzną i jednokrotną w obszarze D, przy czym obraz tego obszaru w przekształceniu w =f(z) oznaczamy symbolem D' (rys. III. 19). W obszarze D wybieramy dowolnie punkt z₀ e D i wyprowadzamy z tego punktu otwarty łuk zwykły o równaniu

z = A(f),    t g <«, /?>    (01.89)

przy czym 2(a)*=Z(,. Zakładamy przy tym, ie istnieje pochodna prawostronna A'(a+) # 0, co zapewnia istnienie jednostronnej stycznej do łuku (111.89) w punkcie z„. Odwzorowanie w =/(z) przekształca łuk (III.89) na otwarty łuk zwykły w = /I(ł),    fe< ct,/S>    (01.90)

przy czym A(a) = /(z₀) =    .

Wykażemy, żc istnieje różna od zera pochodna prawostronna /l'(*+)- Rozważmy dodatni przyrost At parametru t taki, te a+Ai < p, utwórzmy Iloraz różnicowy

AA _ A{tt-\-At)—A(a)

At ⁼ At i przekształćmy go następująco

AA _ /[A(«-Mt)]-/[*«)3 _ f{z₀+Az)—f(z₀) Az At    At    Az    At

gdzie Az = A(a-fdl)—A(«). Zauważmy, ie Az<£ 0, ponieważ hik 00.89) jest zwykły. Stąd

A\a+) =/•(*•) *'<«+) (01.91)