0458

459

§ 1. Przedstawienie analityczne krzywych i powierzchni

Powstawanie tych krzywych można sobie wyobrazić w następujący sposób. Weźmy okrąg o średnicy a. Jeżeli jako biegun obierzemy punkt okręgu i oś biegunową przeprowadzimy przez jego środek S, to dla dowolnego punktu M' tego okręgu będzie r=a cos 6. Jest to równanie biegunowe okręgu. Gdy 0 w równaniu zmienia się od 0 do 27t, to zmienny punkt opisze okrąg dwukrotnie w kierunku przeciwnym do ruchu wskazówek zegara.

Jeżeli się teraz przedłuży wszystkie promienie wodzące OM' okręgu o stały odcinek MM'= b (b> 0), to otrzymane w ten sposób punkty utworzą nową krzywą, którą nazywa się ogólnie ślimakiem. Jej równaniem biegunowym jest oczywiście równanie r=a cos 8+b.

Najprostszy przypadek otrzymujemy, gdy b> a, bo wówczas dla każdego punktu promień wodzący jest dodatni i krzywa otacza biegun ze wszystkich stron (rys. 125a). Gdy b<a, to krzywa przechodzi przez biegun i przecinając samą siebie tworzy wewnętrzną pętlę, jak na rys. 125b. Dla znalezienia kątów 0, dla których zmienny punkt przechodzi przez biegun, podstawmy w równaniu krzywej r=0. Otrzymujemy równanie cos 8 = —b/a, które ma rozwiązanie, ponieważ b<a.

Szczególnie interesujący jest pośredni typ krzywej odpowiadający wartości b=a. W tym wypadku biegun leży na krzywej (8=ii), ale nie ma pętli; krzywa przedstawiona jest na rys. 125c. Od razu rzuca się w oczy, że krzywa ta jest kardioidą, rozpatrywaną wyżej jako szczególny przypadek epicykloidy (rys. 120). Sprawdzenie tego pozostawiamy czytelnikowi.

Przykład 5. Lemniskata Bernoulliego r¹ = 2a² cos 28 (rys. 126).

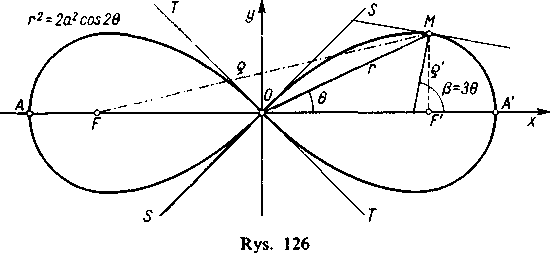
Krzywą tę można określić jako miejsce geometryczne punktów M, dla których iloczyn odległości p = FM, p' = F’M od dwu danych punktów F i F' odległych od siebie o 2a, jest wielkością stałą, równą a² (¹).

Przy oznaczeniach przyjętych na rysunku, z trójkątów OMF i OMF' mamy p² = r² + a² + lar cos 0,    p'² — r² + a²—lar cos 8,

zatem zgodnie z definicją lemniskaty

p²p'² = (r² + a²)² —4a²r² cos² 6 — a¹

Stąd po elementarnych przekształceniach otrzymujemy

r² —2a² cos 20.

Jest to biegunowe równanie lemniskaty.

Ponieważ lewa, a wraz z nią i prawa strona tego równania nie może przybierać wartości ujemnych, więc kąt 8 może przybierać wartości tylko z takich przedziałów, dla których cos 20>O. Są to przedziały (0, itt), (jR, tli), (^t, 2tt).

1

Przy tej zależności między odległością FF' i wielkością iloczynu pp' środek O odcinka FF' leży na krzywej (p=/>'=«). Inaczej jest, gdy pp' = b² i b^a. Otrzymuje się wówczas tak zwane owale Cas-siniego.