0464

465

§ 1. Przedstawienie analityczne krzywych i powierzchni

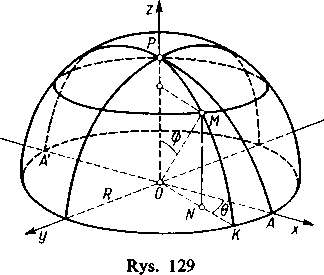
Chcąc otrzymać jej zwykłe przedstawienie parametryczne poprowadźmy przekrój „równikowy” AKA', a przez „bieguny” P i P' i rozpatrywany punkt M poprowadźmy „południk” PMKP’. Położenie punktu M na sferze może być określone kątami <p=%.POM i 0 = -^AOK. Jest teraz z=NM=R cos ę oraz ON= R sin ę. Współrzędne x i y, takie same dla punktu M jak i dla N, można wyrazić przez ON wzorami x=ONcos 0, y = ONsin 9. Zestawiając znalezione zależności otrzymujemy parametryczne równanie sfery

x = J?sin (pcosO, y = Rsin <psin0, z = Rcosq>,

przy czym kąt ę wystarczy zmieniać od 0 do n, a kąt 0 od 0 do 2n.

Odpowiedniość między punktami sfery i punktami prostokąta <0, n; 0, 2n> na płaszczyźnie <p0 nie jest wzajemnie jednoznaczna (‘). Wartości 0=0 i 0=2n prowadzą bowiem do tych samych punktów powierzchni, a ponadto dla ę=0 (lub ę> = n) otrzymujemy jeden tylko punkt — biegun P (lub P‘) niezależnie od tego, jaka jest wartość 0.

Jeżeli kąt f zastąpimy kątem X = łn — <p zmieniającym się od — ±n do j-ir, a dla kąta 0 weźmiemy przedział zmienności od — n do n, to otrzymamy znane współrzędne geograficzne — szerokość geograficzną i długość geograficzną.

Dla macierzy pochodnych cząstkowych

wszystkie wyznaczniki

Rcos ęcos 0 —iłsin psinO

R cos <p sin 0 R sin ę cos 0

— R sin 0

1

/{²sin² <dcos0, R² sin² ę sin 0, R² sin q> cos ę>,

są jednocześnie równe zeru dla q> = 0 i <p = n. Jest jednak oczywiste, że obydwa „bieguny” są punktami osobliwymi jedynie przy tym analitycznym przedstawieniu sfery, które właśnie rozpatrujemy.

Łatwo dostrzec, że jedna rodzina linii współrzędnych na sferze jest utworzona z południków 0=const, a druga — z równoleżników <p = const.

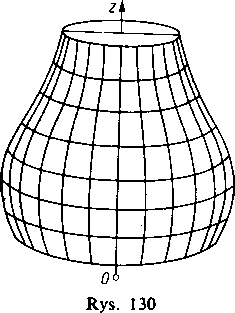
4) Poprzedni przykład można uogólnić w następujący sposób. Niech będzie dana w płaszczyźnie xz krzywa (zwana tworzącej o równaniach parametrycznych

(16)    x=ę>(u),    z = i//(u),

przy czym ?(u)>0. Obracajmy tę krzywą, jak ciało sztywne, dokoła osi z (rys. 130). Jeżeli przez v oznaczymy kąt obrotu, to równania otrzymanej w ten sposób powierzchni obrotowej będą miały postać

x = q>(u) cosv,    y=<p(u) siny,    z=i//(u)    (0<t><2n).

(') Patrz notka na dole str. 463.

30 G. M. Ficbienholz