0454

455

§ 1. Przedstawienie analityczne krzywych i powierzchni

W przypadku hipocykloidy można w podobny sposób otrzymać następujące równania parametryczne:

x=a [(1— m)cosm/+mcos(l — m)t], y=a [—(1— m)sinmt+msin(l— m)t].

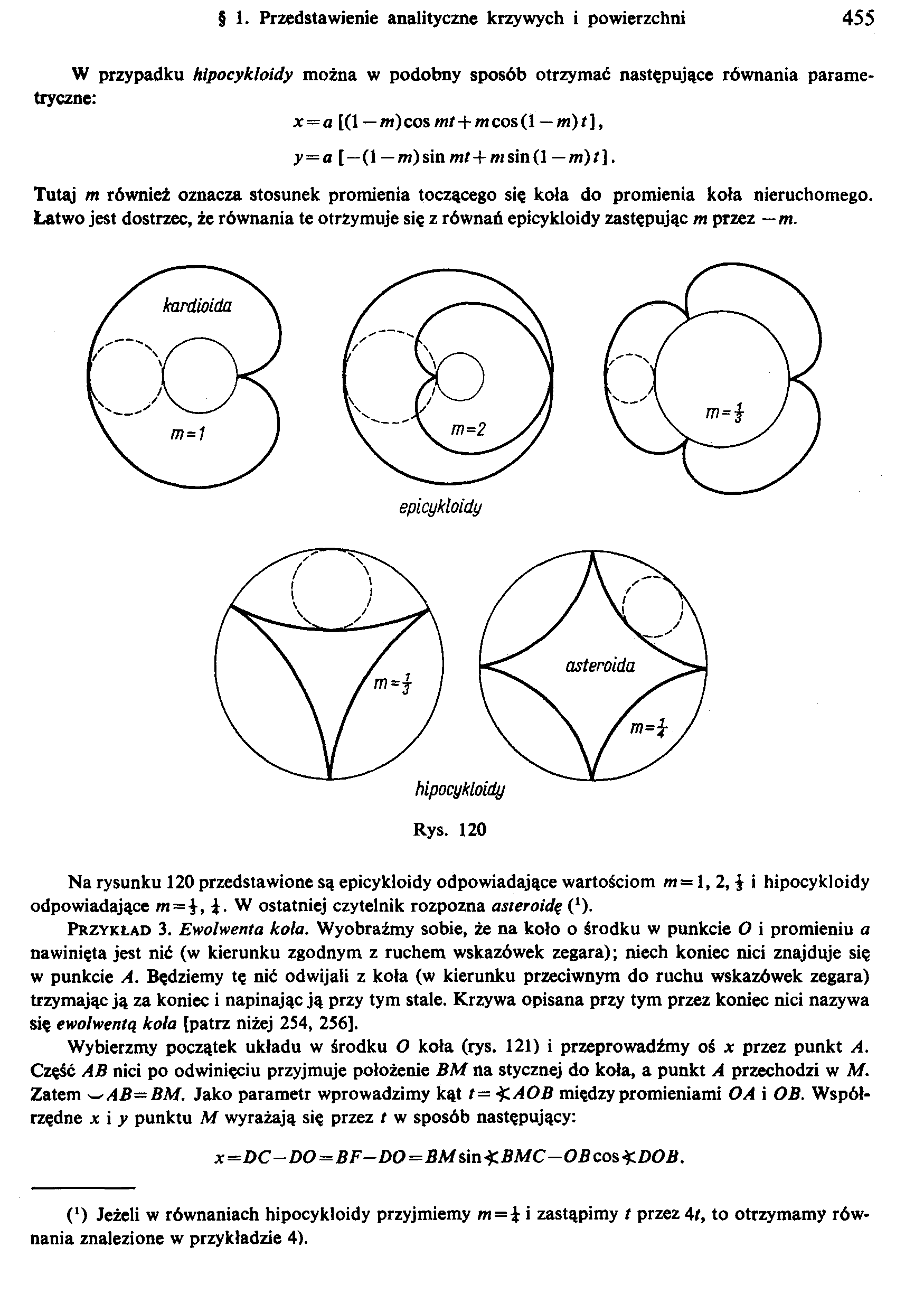
Tutaj m również oznacza stosunek promienia toczącego się koła do promienia koła nieruchomego. Łatwo jest dostrzec, że równania te otrzymuje się z równań epicykloidy zastępując m przez — m.

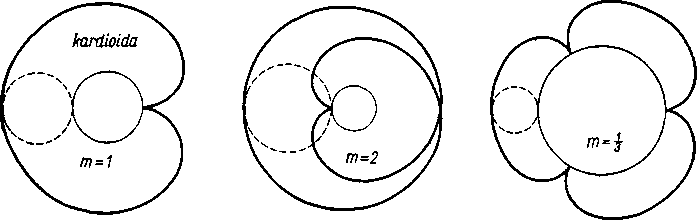
epicykloidy

Na rysunku 120 przedstawione są epicykloidy odpowiadające wartościom m= 1, 2, $ i hipocykloidy odpowiadające m = ł, £. W ostatniej czytelnik rozpozna asteroidę (‘).

Przykład 3. Ewolwenta koła. Wyobraźmy sobie, że na koło o środku w punkcie O i promieniu a nawinięta jest nić (w kierunku zgodnym z ruchem wskazówek zegara); niech koniec nici znajduje się w punkcie A. Będziemy tę nić odwijali z koła (w kierunku przeciwnym do ruchu wskazówek zegara) trzymając ją za koniec i napinając ją przy tym stale. Krzywa opisana przy tym przez koniec nici nazywa się ewolwentą koła [patrz niżej 254, 256].

Wybierzmy początek układu w środku O koła (rys. 121) i przeprowadźmy oś x przez punkt A. Część AB nici po odwinięciu przyjmuje położenie BM na stycznej do koła, a punkt A przechodzi w M. Zatem -^AB=BM. Jako parametr wprowadzimy kąt t= $.AOB między promieniami O A i OB. Współrzędne x i y punktu M wyrażają się przez t w sposób następujący:

x—DC—DO=BF—DO=BM&m%.BMC—OB cos *DOB.

(') Jeżeli w równaniach hipocykloidy przyjmiemy m = i i zastąpimy t przez 41, to otrzymamy równania znalezione w przykładzie 4).