0460

461

§ 1. Przedstawienie analityczne krzywych i powierzchni

Zajmijmy się teraz krzywymi w przestrzeni. Najprościej można określić krzywą w przestrzeni przedstawiając dwie współrzędne, na przykład y i z, jako funkcje trzeciej współrzędnej x:

(9)

y=f(x),    z = g(x).

Takie przedstawienie krzywej jest naturalną analogią nieuwikłanego przedstawienia krzywej na płaszczyźnie. Równania typu (9) można by było nazwać nieuwiklanymi równaniami krzywej. Podobnie jak w przypadku krzywej płaskiej do takiego przedstawienia sprowadzają się w zasadzie wszystkie inne analityczne przedstawienia krzywej przestrzennej.

Każde z równań (9) może być interpretowane bądź jako równanie rzutu krzywej na odpowiednią płaszczyznę Oxy lub Oxz układu współrzędnych, bądź jako równanie rzutującego walca (patrz (8)) o tworzących równoległych odpowiednio do osi z lub do osi y.

Ogólniejszy sposób określenia krzywej przestrzennej polega na tym, że rozpatruje się ją jako przecięcie dwóch dowolnych powierzchni. Jeżeli powierzchnie te są określone równaniami

(10)

F(x,y,z) = 0 i G(x,y,z) = 0

(każda powierzchnia jednym równaniem), to układ tych dwu równań jest przedstawieniem analitycznym krzywej ich przecięcia. Równania (10) nazywamy równaniami uwikłanymi krzywej.

Utwórzmy macierz z pochodnych cząstkowych funkcji Fi G:

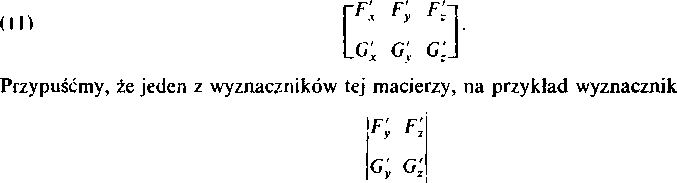
jest różny od zera w rozpatrywanym punkcie. Wówczas na podstawie twierdzenia IV z ustępu 208 w otoczeniu tego punktu równania (10) można zastąpić równaniami typu (9), przy czym występujące w tych równaniach funkcje są także ciągłe wraz ze swoimi pochodnymi.

Tym samym możliwość sprowadzenia do najprostszego sposobu przedstawienia nie jest zagwarantowana tylko w otoczeniu takiego punktu krzywej, w którym wszystkie trzy wyznaczniki macierzy (11) są jednocześnie równe zeru. Punkty takie nazywamy punktami osobliwymi.

228. Przedstawienie parametryczne. Zajmiemy się na zakończenie parametrycznym przedstawieniem powierzchni i krzywych w przestrzeni zaczynając tym razem od krzywych.

Podobnie jak w przypadku krzywej płaskiej, współrzędne zmiennego punktu krzywej przestrzennej mogą być dane jako funkcje pewnej pomocniczej zmiennej — parametru /:

(12)

x=<p(t), y — y/(t), z = y(t).