0452

453

§ 1. Przedstawienie analityczne krzywych i powierzchni

Przy r-> oo obie współrzędne dążą do O, można więc przyjąć, że punkt (O, 0) otrzymuje się dwukrotnie — dla t=0 i dla t= oo. Gdy t zmienia się od — oo do —1, to punkt (jc, y) wychodząc z punktu (O, 0) oddala się po prawej gałęzi krzywej do nieskończoności; gdy t zmienia się od — 1 do 0, to punkt ten wraca z nieskończoności po levyej gałęzi do punktu (0, 0); wreszcie przy wzrastaniu I od 0 do -4- co punkt przebiega pętlę w kierunku przeciwnym do ruchu wskazówek zegara.

225. Krzywe pochodzenia mechanicznego. W dalszym ciągu tego przeglądu krzywych rozpatrzymy jeszcze pewne krzywe pochodzenia mechanicznego, otrzymywane przez toczenie się jednej krzywej po drugiej.

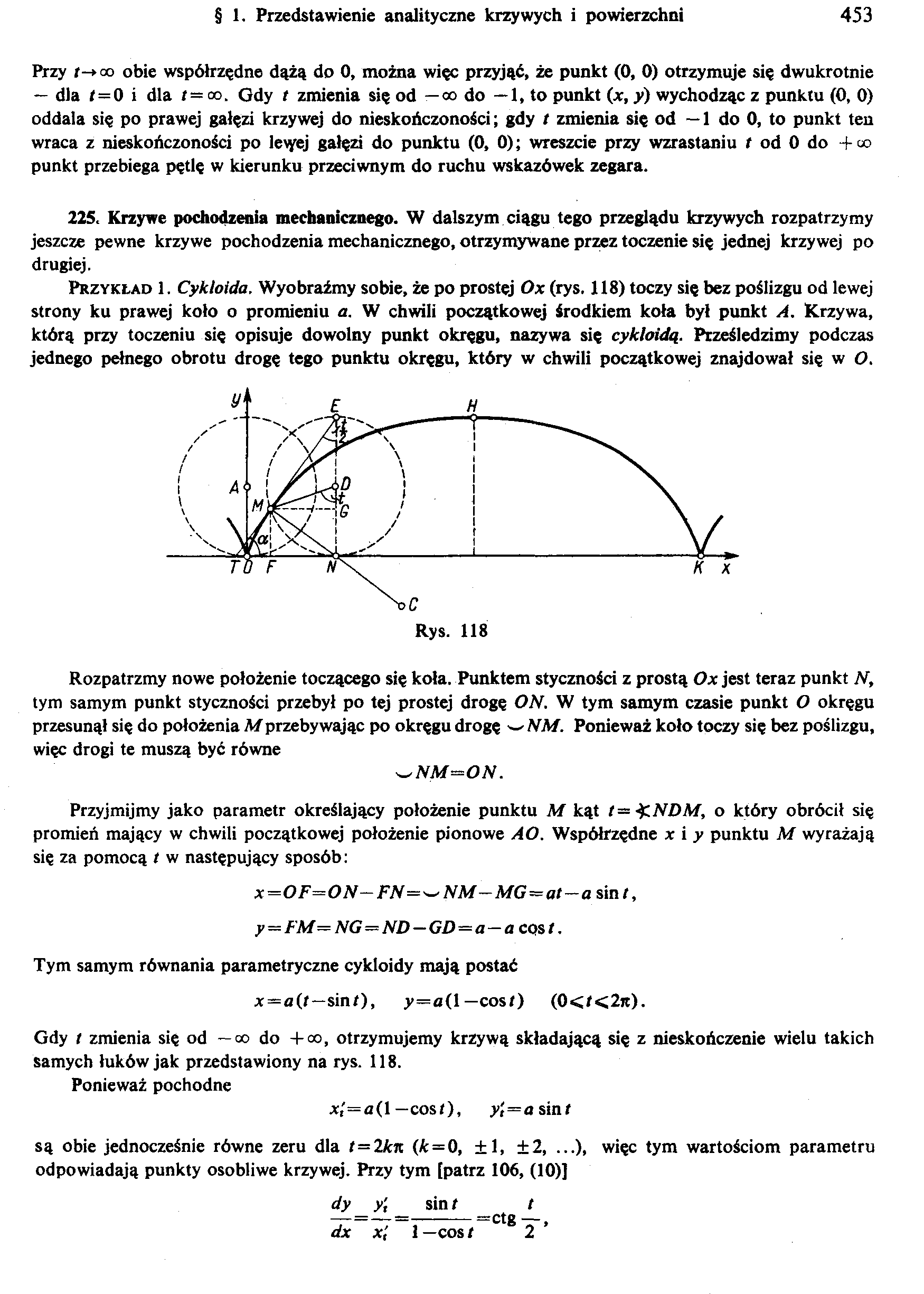
Przykład 1. Cykloida. Wyobraźmy sobie, że po prostej Ox (rys. 118) toczy się bez poślizgu od lewej strony ku prawej koło o promieniu a. W chwili początkowej środkiem koła był punkt A. Krzywa, którą przy toczeniu się opisuje dowolny punkt okręgu, nazywa się cykloidą. Prześledzimy podczas jednego pełnego obrotu drogę tego punktu okręgu, który w chwili początkowej znajdował się w O.

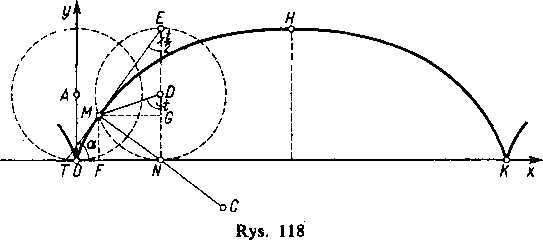
Rozpatrzmy nowe położenie toczącego się koła. Punktem styczności z prostą Ox jest teraz punkt N, tym samym punkt styczności przebył po tej prostej drogę ON. W tym samym czasie punkt O okręgu przesunął się do położenia M przebywając po okręgu drogę w NM. Ponieważ koło toczy się bez poślizgu, więc drogi te muszą być równe

^NM—ON.

Przyjmijmy jako parametr określający położenie punktu M kąt t= ^.NDM, o który obrócił się promień mający w chwili początkowej położenie pionowe AO. Współrzędne x i y punktu M wyrażają się za pomocą t w następujący sposób:

x=OF=ON—FN—^NM—MG=at—a sini, y — FM— NG—ND —GD —a —a cqs<.

Tym samym równania parametryczne cykloidy mają postać

x—a(t—sin/),    y=a(l — cost) (0</<2it).

Gdy t zmienia się od — oo do +oo, otrzymujemy krzywą składającą się z nieskończenie wielu takich samych łuków jak przedstawiony na rys. 118.

Ponieważ pochodne

•x,'=a(l — cost), y;=asinf

są obie jednocześnie równe zeru dla t=2kn (k = 0, ±1, ±2, ...), więc tym wartościom parametru odpowiadają punkty osobliwe krzywej. Przy tym [patrz 106, (10)]

t    ₄    « »

dx x_t 1 —cos t    2