0456

457

§ 1. Przedstawienie analityczne krzywych i powierzchni

Przejdźmy do przykładów.

Przykład 1. Spirala Archimedesa r=aO (rys. 122).

Krzywą tę można rozpatrywać jako trajektorię punktu poruszającego się ruchem jednostajnym po wychodzącej z bieguna półprostej, która jednocześnie obraca się również jednostajnie dokoła bieguna.

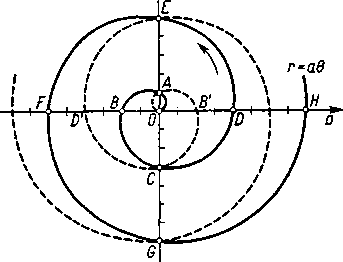
Rys. 122

Aby odnaleźć ciąg punktów A, B,C,D, ... krzywej, którym odpowiadają kąty Jn, 2-in, 3-ijt, 4-jrr itd., odłóżmy na prostej pionowej odcinek OA = a-in, a następnie weźmy 0B=20A, 0C=30A, 0D=40A, itd. Zmieniając kąt 9 od 0 do oo otrzymujemy nieskończony ciąg zwojów krzywej OABCD, DEFGH, ... Odległości między punktami sąsiednich zwojów mierzone wzdłuż promienia są równe 2na.

Kątowi 9 można nadawać też wartości ujemne od 0 do — oo. Otrzymuje się wówczas drugą część krzywej OAB'CD\ ..., oznaczoną na rysunku linią przerywaną. Jest ona symetryczna do pierwszej.

Zauważmy, że równanie r=a9+b też przedstawia spiralę Archimedesa. Jeżeli obrócić oś biegunową o kąt b

a=--, to równanie to sprowadzi się do postaci r— = a9.

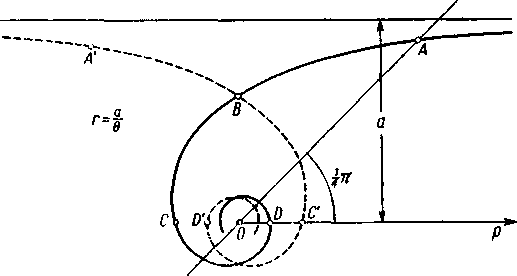
Przykład 2. Spirala hiperboliczna r=—■ (rys. 123).

U

Gdy kąt 9 rośnie do nieskończoności, to promień wodzący dąży do zera i punkt krzywej dąży do bieguna, nigdy go nie osiągając. W tym przypadku biegun jest tak zwanym punktem asymptotycznym krzywej. Krzywa zwija się nieskończenie wiele razy dokoła bieguna.

Rys. 123

Jeśli na promieniu 9=in odłożymy odcinek OA—4aln i następnie na promieniach 9=iit, n, 2n.....

odłożymy odcinki OB-iOA, OC-iOB, OD=\OC, ..., to punkty A, B, C, D, ... będą oczywiście leżały na krzywej.

Kąt 9 może przybierać również wartości ujemne. Gdy 9 się zmienia od 0 do — oo, to podobnie jak dla spirali Archimedesa otrzymuje się drugą część krzywej A'BC’D' .... symetryczną do pierwszej. Na rysunku jest ona zaznaczona linią przerywaną.