0450

451

§ 1. .Przedstawienie analityczne krzywych i powierzchni

Można oczywiście posłużyć się jakimikolwiek innymi wyrażeniami, których suma kwadratów jest równa jedności, na przykład przyjąć

1 -u

1 +«“

y=b

2 u

1+u¹'

Tutaj u zmienia się od — oo do +oo. Gdy u-> ± co, to x-*—a, y-*0, zatem można umownie przyjąć, że punkt A' (—a, 0) otrzymuje się dla u= ± oo.

Analogicznie w przypadku hiperboli

-__L=i

_2 ł2 ¹

funkcje kosinus hiperboliczny

korzystając ze znanej zależności wiążącej i sinus hiperboliczny można przyjąć

(— oo<f< + oo).

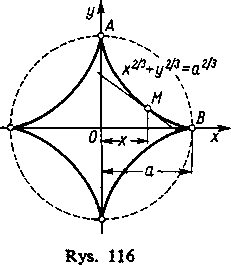
x — a coshr.

Inną parametryzacją tej krzywej jest

x=a

l+«² 1 -u¹’

y = b

2 u

1 -u¹

(— oo<«< + oo ; u#±l).

Czytelnikowi zalecamy zorientowanie się jak przebiega punkt po krzywej przy zmianie parametru.

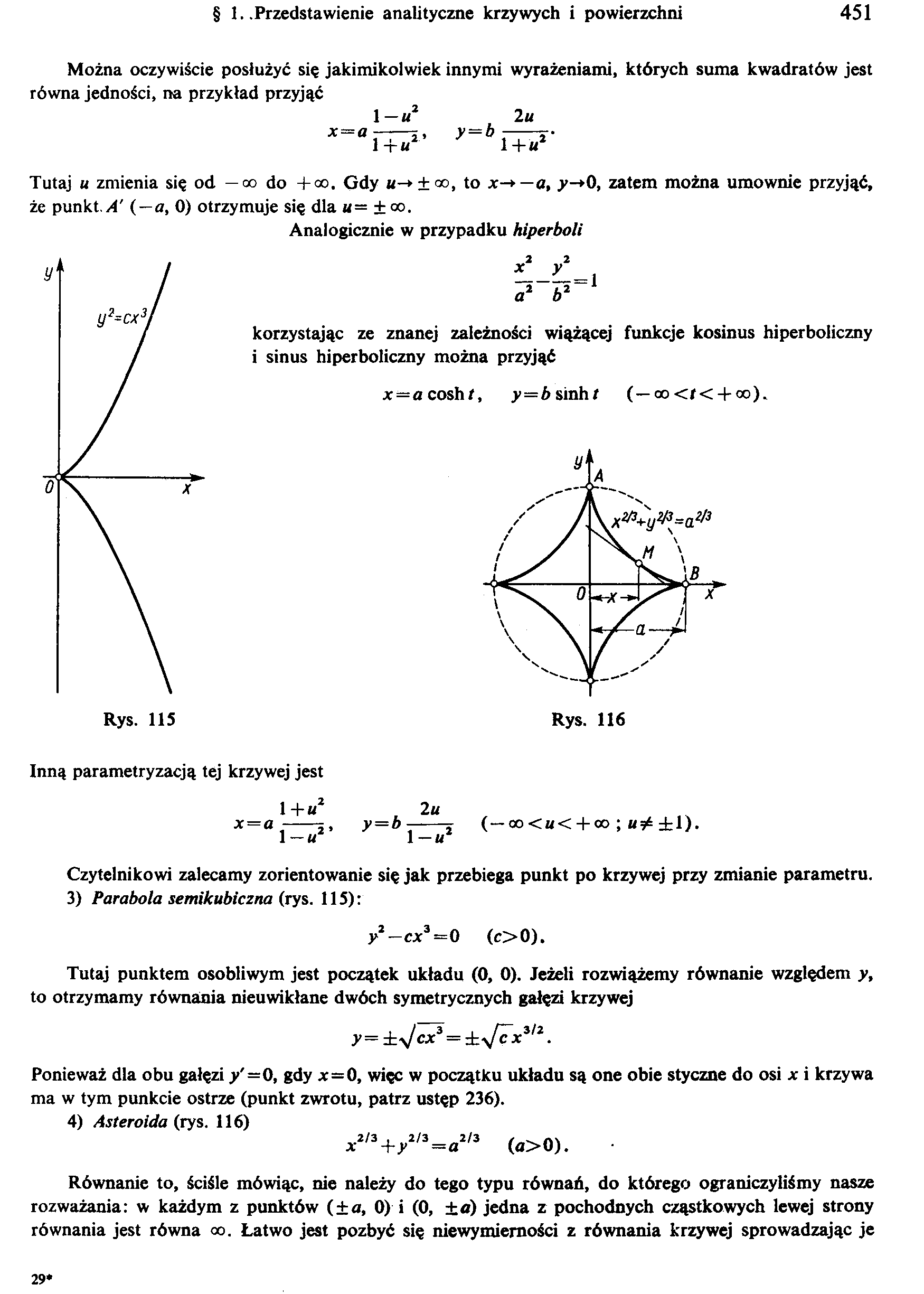
3)    Parabola semikubiczna (rys. 115):

y²—cx³ = 0    (c>0),

Tutaj punktem osobliwym jest początek układu (0, 0). Jeżeli rozwiążemy równanie względem y, to otrzymamy równania nieuwikłane dwóch symetrycznych gałęzi krzywej

y = ±\Jcx³ = ±*fcx^il2.

Ponieważ dla obu gałęzi y'—0, gdy *=0, więc w początku układu są one obie styczne do osi x i krzywa ma w tym punkcie ostrze (punkt zwrotu, patrz ustęp 236).

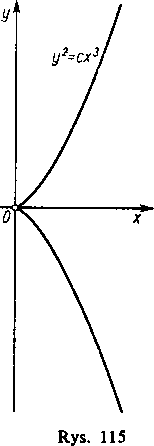
4)    Asteroida (rys. 116)

x^2l3+y^2,3=a¹¹³    (a> 0).

Równanie to, ściśle mówiąc, nie należy do tego typu równań, do którego ograniczyliśmy nasze rozważania: w każdym z punktów (±a, 0) i (0, ±«) jedna z pochodnych cząstkowych lewej strony równania jest równa oo. Łatwo jest pozbyć się niewymierności z równania krzywej sprowadzając je

29*