4

6) Wyznaczyć sumy szeregów potęgowych :

oo

fe“f*¹"‘ d) E ~^L'⁴"-¹

n=*l    n~ 1    «~1    n~\

_ 1

a) 2>v, b)    c) ES^¹"²    <») E

7)    Rozwinąć funkcję /(x) = 4" w szereg Taylora o środku w punkcie :

a) x₀ = 1,    b) x₀ = -2 .

8)    Rozwinąć funkcję J{x) w szereg Taylora o środku w punkcie x₀ , jeśli

a) A*) =

1

JC+1

jc+2

, x_G = 2 .

9)    Korzystając z rozwinięcia funkcji wykładniczej w szereg Maclaurina wykazać, że

5    oo

{ -ędx = ln2 + E (-0’fj-

¹    i    ^

10)    Przedstawić całkę J --^cf—dx jako sumę szeregu liczbowego.

Ile należy wziąć wyrazów otrzymanego szeregu, aby obliczyć daną całkę z dokładnością do 0,01 ?

2 oo

11) Uzasadnić wzór J (Z xⁿ)dx -ę^dx , a następnie obliczyć sumę

o »=i    o

szeregu liczbowego ^    ■

n=\

12) Metodą rozwinięcia w szereg obliczyć całki:

c) |    ,

0 x

d) | cos t³dx .

o

13) Korzystając z rozwinięcia funkcji f{x) =    w szereg Fouriera wyznaczyć

oo

E(— 1) ^W+1

n= 1

00

14) Obliczyć sumę szeregu ^    ^ --₂ korzystając z rozwinięcia funkcji /(x) = |x|

\Zn i)

n-1

w szereg Fouriera w przedziale < -n,n > . Jaką funkcję przedstawia otrzymany szereg dla e ?

15) Rozwinąć funkcję f{x) = x³ w szereg Fouriera w przedziale <-n,n>. Wykorzystać otrzymane rozwinięcie do obliczenia sum szeregów

00    oo

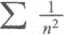
v (-0"

n= 1    »=1

1

o

2

3

a) J e~^x2dx,