54

104

pozycji zliczonej. Pozycje obserwowane, nanoszone obok linii zliczenia drogi statku, służą do kontroli zliczenia, wnioskowania o wy stępowaniu znosu i dryfu.

104

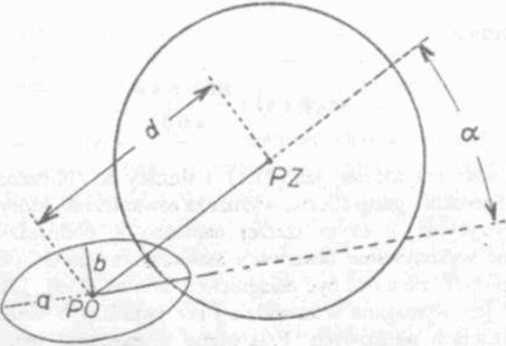
Ryv$ I Kierunkowy Mąd pozycji; d oznacza wyłącznie odległość. a nic kierunkowy błąd jak w (5.2)

Decyzje o korekcie zliczenia muszą być oparte na analizie obserwacji, ocenie pozycji obserwowanej i wzajemnej relacji pól błędu zliczenia i obserwacji. Głównym warunkiem poprawności zliczenia i pozycji obserwowanej jest wzajemne nakładanie się (częściowe) granicznych pól błędu (elipsy lub koła). Gdy ten warunek nie jest spełniony, oznacza to uchybienia w zliczeniu bądź błąd gruby w pozycji obserwowanej. Na rysunku 5.1 przedstawiono sytuację pól błędów częściowo pokrywających się. Rozpatruje się wówczas kierunkowy błąd pozycji. Należy określić wartość d graficznie jak na rysunku 5.1 lub obliczyć ze wzoru:

(5.2)

d² = a² cos² a ♦ b² sin² a

gdzie a i b to półosie elipsy błędu pozycji.

Prawdopodobieństwo błędu wektorowego (d) wynosi 68,3%, zaś błąd średni pozycji oblicza się z zależności:

^dsi * ^    (5.3)

gdzie M oznacza radialny błąd pozycji.

Punkt prawdopodobny (pozycja estymowana) wyznaczona z dwóch pozycji (zliczonej i obserwowanej) znajduje się bliżej pozycji o mniejszym polu błędu i dzieli odcinek łączący obie pozycje proporcjonalnie do kwadratów błędu (jak we wzorach (3.l7)).Ocena błędu większej liczby punktów oznaczających pozycje obserwowane może być rozpatrywana w kolejnych parach. Stosowanie takich algorytmów w automatycznych obliczeniach powoduje ciągłe poprawianie (aktualizowanie) pozycji sutku. Przytoczony sposób korekty jest równoważny sprowadzeniu do wspólnego zenitu wszystkich linii pozycyjnych. W wyniku tego sprowadzenia niezależne linie pozycyjne stają się liniami zależnymi, obciążonymi błędami zliczenia. Ich współczynniki korelacji sują się różne, co powoduje komplikacje z ich wyrównaniem [5).

Bieżąca korekcja pozycji (ulepszanie) może być całkowicie zautomatyzowana. Linie pozycyjne są niezależne. Macierz korelacyjna sprowadzona jest do postaci diagonalnej i błędy prze-kształcają się w niezależne. Informacja nawigacyjna zawiera zwykle następujące cztery liczby: dwie współrzędne pozycji, poprawkę prędkości i znos sutku. Trzeba też w tym celu dostarczyć co najmniej cztery parametry nawigacyjne (mogą to być cztery alp). Parametry nie mogą być mierzone jednocześnie, ponieważ wymagane jest określenie średnich wartości prędkości i kursu (postulat niejednoczesności).

Jednoczesne rozwiązanie kilku linii pozycyjnych polega na zastosowaniu algorytmu wyrównania i nazywa się filtracją. Stosując kolejno linie pozycyjne według pewnej rekurencyjnej procedury można osiągnąć dopływ informacji w czasie rzeczywistym. Informacje tego rodzaju opracowuje komputer. Taką filtrację nazywa się kalmanowską, a jej idea jest pomysłem Gaussa.