302 (15)

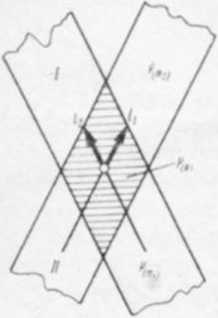
Równoległobok najbardziej obrazowo ilustruje rozkład pozycji obserwowanej. Jeżeli się założy, że obie linie pozycyjne mają rozkład normalny, to prawdopodobieństwo P_imX znalezienia się obserwatora w pasie pozycyjnym o szerokości im wynosi 0,68 dla obu linii. Prawdopodobieństwo P_{R) znalezienia się obserwatora na powierzchni równoległobok u powstałego z przecięcia się dwóch linii pozycyjnych jest równe iloczynowi prawdopodobieństw obu pasów (rys. 15.25). czyli P_{K) — 0,68x <0.68 = 0,46 Oznacza to, że na 100 pozycji obserwowanych 46 pozycji będzie leżało na powierzchni równo-Icgłoboku.

W praktyce najczęściej stosuje się elipsę błędów, ponieważ figura ta najwierniej charakteryzuje rozkład pozycji.

Rys. 15.25. Równoległobok błędów z dwóch linii poz>cyjn>ch (/,. /j — wektory błędów linii pozycyjnych)

Najłatwiej ocenia się dokładność pozycji za pomocą promienia koła.

Przy obliczaniu dokładności pozycji dowolnym sposobem należy za każdym razem wyznaczać prawdopodobieństwo znajdowania się pozycji obserwowanej w określonym obszarze.

Elipsa błędów

W miejscu przecięcia się linii pozycyjnych, mających rozkład normalny, powstaje figura przestrzenna przedstawiająca rozkład błędów pozycji dwóch zmiennych Przeprowadzając płaszczyznę przez punkty przegięcia powierzchni tej figury, otrzymuje się elipsę błędów (rys. 15.26). Jeżeli dane są błędy średnic m_x i m₂ linii pozycyjnych oraz kąt ich przecięcia się oznaczony prz.cz AA = A ₂ —A,, to można obliczyć moduły błędów wektorowych równoległoboku. Jak widać z rys. 15.27, moduły błędów wektorowych /, i l₂ wynoszą

.    I,    (I5.3IT

sin AA

(15.32)

”*2

sin AA

Z geometrii analitycznej wynikają związki między modułami błędów wektorowych w równoległoboku a osiami elipsy wpisanej w ten równoległobok. Wyrażają się one następująco:

ll + ll = a² + b²,    (15.33)

_mab - t_Ł-l₂-mAA.    (15.34)

gdzie a jest dużą półosią elipsy, b zaś małą półosią elipsy.

302