DSC00088 (2)

F(y,y',y")sO | równanie nie zawiera zmiennej niezależnej x. dstawiamy: /^(y), wtedy:

y"=v'(y)y'=v'v

iwnanie przyjmie postać: Fty.y.w')^. zykład 9.

ozwiązać równanie: 2yy” =(y*)² + y².

\z'fy) -y ' vV- v j ²

- V V

JjBj ii ic$+

te) v'~j^-v= 4,

i) ? 3u~ ~ V §S

3

MS

*'(y)=JVv'

ml u

^

<fc -^ ~ 5 WWIr

i *Vu ²J*% - Ju VM*o

5P¹*

«v'vł\‘e ^

'Mioue

Wilij(+ Ui(G-j

i r
u elu^) ti\Js
*= CTo>m L*'* *	^cca>'>
:^c r3^/3’^1 c<y-	i'^c

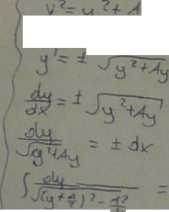
[M 'yś+j^s

v= *

3'M₃/=J

O

Oj**;.,

M«T2M_Mhatror.lk_Bj«_nNllwrookl