image 041

Założenia wstępne - koncepcja strefy dalekiej 41

styczna pola elektrycznego, składowa zaś styczna pola magnetycznego równa jest gęstości prądu powierzchniowego. Ostatnia uwaga dotyczy zachowania się wektorów pól: elektrycznego i magnetycznego w pobliżu nieciągłości (osobliwości) np. klina wykonanego z idealnego przewodnika, o kącie wewnętrznym (po (rys. 2.2a) Problem ten jest szczególnie ważny w sytuacji powszechnego wy-

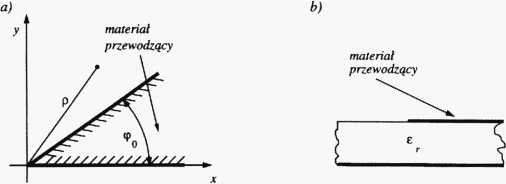
Rys. 2.2. Przykładowe nieciągłości z materiałem przewodzącym: a) klin przewodzący, b) krawędź paska przewodzącego w strukturze niesymetrycznej linii paskowej

korzystywania metod numerycznych (np. metody momentów - patrz rozdział 6), których efektywność zależy od prawidłowego założenia kształtu poszukiwanych składowych pól (prądów). Przykładowo, w antenach realizowanych techniką planarną [3] mamy często do czynienia z nieciągłością w postaci krawędzi przewodzącej ((po = 0, rys. 2.2b). Można pokazać [5], że składowe pól e-m normalne do krawędzi przewodzącej (oznaczone tutaj jako H_n,E_n) mogą być nieograniczone w bezpośredniej bliskości osobliwości, przy czym rząd tej osobliwości jest taki, że suma energii zmagazynowanej w polach: elektrycznym i magnetycznym pozostaje skończona. Ten ostatni warunek pozwala określić rząd osobliwości i przykładowo dla struktury z rys. 2.2a uzyskuje się:

E_n,H_n ~ p^a    (2.9)

przy czym najmniejsza wartość parametru a wynosi -0,5. Znajomość wsp. a w przypadku pól magnetycznych pozwala określić rząd osobliwości prądów powierzchniowych płynących w bezpośredniej bliskości krawędzi.

W przypadku ośrodków nieograniczonych, a z takimi mamy zwykle do czynienia w technice antenowej, uzyskane przez nas rozwiązania muszą spełniać tzw. warunek wypromieniowania [2] (warunek Sommerfelda ). Z warunku tego dla ośrodka bezstratnego widać, że jeśli źródło promieniowania znajduje się w początku układu współrzędnych, to w dużej odległości od źródła pole maleje co najmniej jak r~^l, a faza jest taka sama jak u fali odchodzącej do nieskończo-