Mechanika ogolna0085

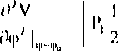
i I',(li i iiJ wm(t|t_(l) «()

Wynika stąd, żc równowaga stulyc/.im występuje dlii <|>₍₎    0. Zatem /, równania

(2) bodziemy mieli: P₂ k-u,,    0.

p

1 )cformacja statyczna sprężmy wyniesie więc: u₀ = —.

k

5.4.7. Równowaga statyczna w polu potencjalnym

Załóżmy, że dany jest układ brył, na który działają siły pola potencjalnego. Potencjał jest funkcją współrzędnych uogólnionych:

V = V(_qi,q₂,...q_s).

Równowaga statyczna wystąpi wówczas, gdy potencjał osiągnie minimalni) wartość dla określonych współrzędnych uogólnionych, czyli:

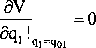
(217)

q.s⁼¹ios

dq_s

Następnie sprawdzamy, czy jest to położenie równowagi trwałej:

(218)

Jeżeli dla określonych współrzędnych uogólnionych spełnione są zależności (217) i (218), to mówimy, że jest to położenie minimum potencjału lub inaczej położenie równowagi statycznej układu (patrz przykład 29).

5.4.8. Równowaga Lagrange'a drugiego rodzaju

Zjawisko ruchu układu można zawsze opisać, stosując tzw. ogólne równanie dynamiki, ale zapiszemy te równania w układzie współrzędnych uogólnionych, mamy wówczas:

(Qi +Qi_B)^sqi =E(Pi ^_mi ‘^¥i)-(⁵^)i ⁼⁰>

i=l

przy założeniu, że: 8q! ^ 0; 8q₂ = Sq₃ =... = 8q_s = 0.

Druga siła uogólniona:

(Q₂ +Q_2B)8q₂ =Ś(Pi ~^mi •ailM ^{= 0}>

i=l

8q₂ * 0; Sq₂ = 8q₃ =... = Sq_s = 0.

Postępując tak dla każdej współrzędnej uogólnionej, dojdziemy do ostatniej:

(Qs + Qs_B)8q_s = Ż(Pi "^mi ■ ®i)■ )_s = °>

i=l

8q_s * 0; 8qj = 8q₃ =... = 8q_s_! = 0.

Zależności te możemy wyrazić w postaci:

(Q, +Q^)6q, = £(!* -m, S,) (Si;). =0    (219)

1=1

W równaniu tym mamy odpowiednio:

Qj — j -ta siła uogólniona,

Qj_B - j-ta uogólniona siła bezwładności,

8q, - j-te uogólnione przesunięcie wirtualne,

(8r;)j - przesunięcie wirtualne i-tego punktu odpowiadające j-temu uogólnionemu przesunięciu wirtualnemu.

Równanie (219) możemy zapisać w prostszej postaci:

(Q_j+Q_jB)5q_j=0    (220)

Z równania (219) wiemy, że: