P3300252

Metoda bisekcji (połowienia)

Założenie: f : [a, b) -*• R, f e C[a, b], f(a)f(b) < 0, tj. f zmienia znak w [a, 6). Z tych założeń (własność Darboux) wynika, że w (a, 6) f ma zero i metoda bisekcji korzysta z tej własności.    *

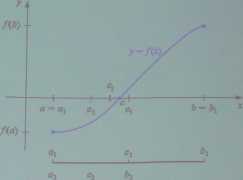
a₃ c₃

Rysunek 2: Metoda bisekcji

Jeśli f(a)f(b) < 0, to obliczamy d = (a+ b)/2 i sprawdzamy, czy f(a)f(c1) < 0. Jeśli tak, to f ma zero w [a, ci] i kładziemy ai = a, b| = c-i. W przeciwnym razie zero jest w [ci, b] i kładziemy a₁ = Cf, bi = b. Nowy przedział jest dwa razy krótszy niż poprzedni i zawiera zero f i postępowanie to można powtórzyć.

©Zbigniew Bartoszewski (Politechnika 3/88