skanuj0035 (4)

215

fi7.1 Określenie funkcji wielu ani&Mty&h

Warstwicą odpowiadającą wartości c funkcji g(x,y) = x² § y² = 1 jest zbiór: I,(c) §{(x,y) e l²: x² + y² + 1 = c}. I

Łatwo zauważyć, że wartości funkcji g spełniają warunek g(x,y) > 1 dla (x,y)sD_g. Zatem dla c< 1, mamy I_g(c) = 0 (zbiór pusty - funkcja nie ma warstwie, gdy c < 1).

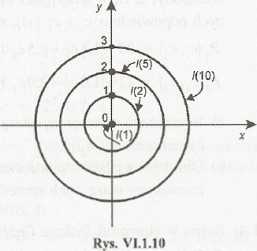
W tym przypadku przekształcone równanie warstwicy do postaci: x² ■+ y² -= c - 1 oznacza, że dla c > 1 warstwice są okręgami współśrodkowymi o promieniach r = <fc - 1 ze środkiem w punkcie (0; 0). Ich położenie dla kilku c ł 1 przedstawiono na rys. VI. 1.10.

ZADANIA VI.l

1.1. Wyznaczyć dziedzinę i obliczyć wymienione wartości funkcji:

a)    /(*) = (x, - l)² t (x₂ * 2)² + *3; /(l; -2; 0), /(-2; -3;2).

b) f(x,y) = —;    /(1; 1), /(-2; 1), /(-2; -1).

c) g(x,y) = (y-x-x²)⁰'⁵;    g( 1;2), g(-2;6), g(-0,5; -0,5).

d)    A(*o>) =    A(-I;c³), %²;-i).

ln(y)

/(-!;!)> /(ln(2);0).

1 -e*^y

e)    /(*,y) = ^9;