skanuj0147

292

mieni 1 i 2 zapisać jako:

a-y

S = asin a = ,    .

■

Z powyżsjzej zależności oraz ze wzoru (2) wynika, że położenie minimów natężenia światła (ciemnych prążków) na ekranie, y„, gdy X< a dane jest równaniem:

(6)

nLX

ja²-n²X² ’

gdzie n jest liczbą całkowitą.

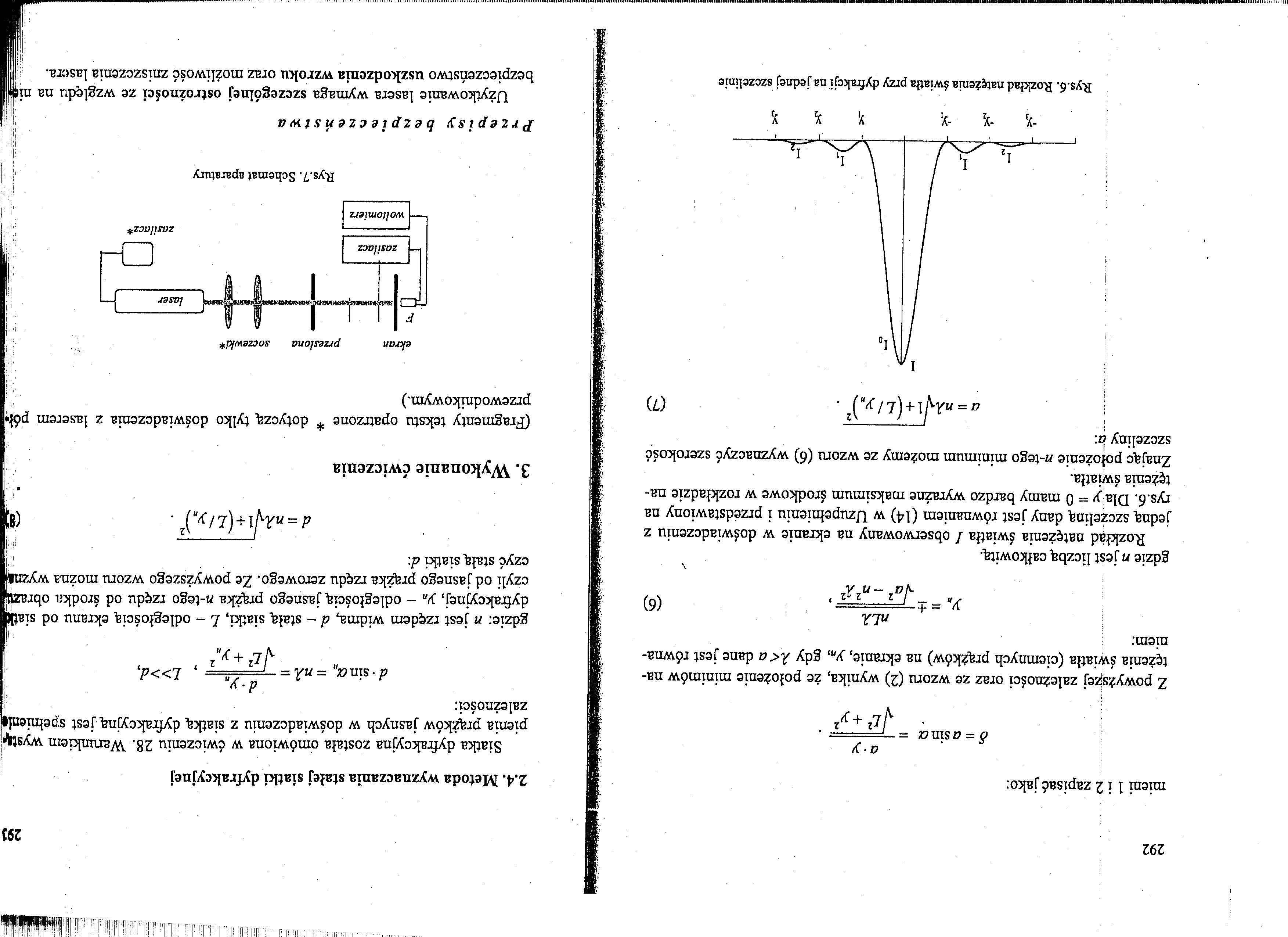
Rozkład natężenia światła / obserwowany na ekranie w doświadczeniu z jedną szczeliną dany jest równaniem (14) w Uzupełnieniu i przedstawiony na rys. 6. Dla y = 0 mamy bardzo wyraźne maksimum środkowe w rozkładzie natężenia światła.

Znając położenie n-tego minimum możemy ze wzoru (6) wyznaczyć szerokość szczeliny a:

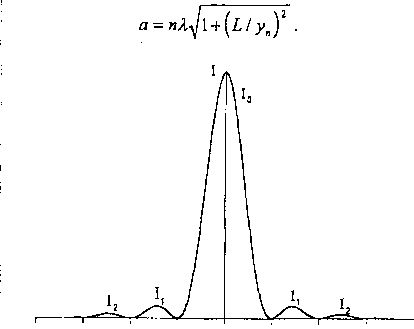
Rys.6. Rozkład natężenia światła przy dyfrakcji na jednej szczelinie

%

2.4. Metoda wyznaczania stałej siatki dyfrakcyjnej

Siatka dyfrakcyjna została omówiona w ćwiczeniu 28. Warunkiem wysty pienia prążków jasnych w doświadczeniu z siatką dyfrakcyjną jest spełnieni! zależności:    j

d ■ y

d • sin a_n =nźi = -7= , L»d,    <

W+y.¹

gdzie: n jest rzędem widma, d - stałą siatki, L - odległością ekranu od siatit dyfrakcyjnej, y„ - odległością jasnego prążka n-tego rzędu od środka obrazt czyli od jasnego prążka rzędu zerowego. Ze powyższego wzoru można wyzni czyć stałą siatki d:    j

d = n^l + (L/y„)² .    (8)

3. Wykonanie ćwiczenia

(Fragmenty tekstu opatrzone * dotyczą tylko doświadczenia z laserem pół* przewodnikowym.)

ekran    przesłona    soczewki*

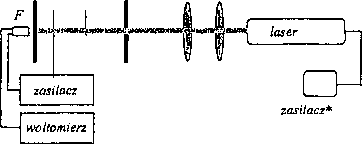
Rys.7. Schemat aparatury

Przepisy bezpieczeństwa

Użytkowanie lasera wymaga szczególnej ostrożności ze względu na nię bezpieczeństwo uszkodzenia wzroku oraz możliwość zniszczenia lasera.

1