Strona0111

111

Qj=-T- </ “ 1. 2.....»)    (5.3)

6q_}

przy czym energia potencjalna układu jest dodatnio określoną formą kwadratową we współrzędnych uogólnionych ze stałymi współczynnikami

^V = \'L^ciMi (U = 1,2,(5.4)

¹ ij=i

gdzie liczby = cji nazywają się współczynnikami sprężystości;

(5.5)

d²V

amj

Energia potencjalna V = V(q_h q₂, q₂, .... #„). Zawsze można przyjąć energię V w takiej postaci, że w położeniu równowagi

F(0,0,..,0) = 0    (5.6)

W położeniu równowagi są również równe zeru uogólnione siły sprężystości (w położeniu równowagi statecznej energia V ma minimum). Przez podstawienie zależności (5.2), (5.3) i (5.4) do równania (5.1), po wykonaniu odpowiednich działań otrzymano równania różniczkowe ruchu w postaci:

a_uq_x+a_nq₂ + ... + a_lnq_n    -ą₂q₂    „fc,

^fl21#I ⁺ a22#2 + — + ^a2n '4n ~ ”^C21#1 “ ^22^2 ” ^_ C2rAn    _(Sr ^

(5.7)

<4\ +a„₂q₂ + ...-ha_nnq_n^-c„₁q_l-c_n2q₂ -...-c_nnq_n ^

Energię kinetyczną lub potencjalną można doprowadzić do sumy kwadratów, czyli przedstawić jako formę kwadratową. Jeżeli do sumy kwadratów jest doprowadzona energia kinetyczna, tj.:

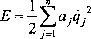
(5.8)

to układ (5.7) przechodzi w układ równań różniczkowych rozprzężonych względem uogólnionych przyspieszeń: