Strona0028

28
Energia potencjalna układu zastępczego przy tym samymą:;_ wynosi
(/=Nje3 (2.20)
Z porównania zależności (2.19) i (2.20) otrzymano Ł - c - ć-. W przypadku rys. 2.3b energię potencjalną obliczono w następujący sposób. Nadano przesunięcie xna końcu sprężyny o współczynniku sprężystości N ■ rys. 2.4).
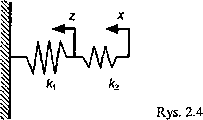
Sprężyna o współczynniku sprężystości k\ została odkształcona o z i energia potencjalna obu sprężyn wynosi
V = +^k2(x~z)2 (2.21)
Ponieważ w punkcie A jest równowaga dwóch sił: k{z = k2(x - z), można z tego równania wyliczyć przesunięcie z:
z =
k2
--—x
kl+k2
Po podstawieniu zależności (2.22) do (2.21) i przekształceniu otrzymano:
v . 1 hki 2 k{ +k2
(2.23)
Z porównania (2.22) i (2.23) otrzymano zastępczy współczynnik sprężystości:
k, —
+ k2
(2.24)
lub w innej postaci
(2.25)
Wyszukiwarka
Podobne podstrony:
Strona0032 32 ¥ (2.28) ±(E + V) = 0 di gdzie: E - energia kinetyczna układu, V- energia potencjalna
Strona0111 111 Qj=-T- </ “ 1. 2.....») (5.3) 6q} przy czym energia potencjalna
Strona0030 30 więc E = — mx2 + —Mx2 = — (m + 0,5M)x2 2 4 2V Energia potencjal
Strona�9 9 Energia potencjalna układu mas Mim: U(r) = ->V„ = GMm[A Pole grawitacyjne jest polem z
_14_Wspomnienie_ Trudno zapomnieć Jego energię i chęć twórczego działania. A przy tym wszystkim był
Strona0209 209 Energia potencjalna V = -/ty2 2 Korzystając z równań Lagrange’a II rodzaju, napiszemy
Strona0228 228 Energia potencjalna wynosi J 2 El J SR, i El
DSC02864 Energia potencjalna układu o masie m, na wysokości h od poziomu umownego E pf=mgh’-0 Praca
mech2 181 560 ty Energia kinetyczna układu 1 .2 1 2 s = T V + T m2 V przy czym+ y2, x2 = x + ł sinty
mech2 181 560 ty Energia kinetyczna układu 1 .2 1 2 s = T V + T m2 V przy czym+ y2, x2 = x + ł sinty
P1020199 Prędkość punktu materialnego: v = /<p Energia potencjalna układu: V = mgz — mg(l -1
P1020199 Prędkość punktu materialnego: v = /<p Energia potencjalna układu: V = mgz — mg(l -1
P1050445 Wnxl.n LKrzywe energii potencjalnej układu Na + Cl Energia (eV) 5 odległość (A) Proces pows
66433 zad1 (24) 6. Obliczyć energię potencjalną układu oraz przesunięcie poziome rygla <5. Do obl
więcej podobnych podstron