Strona0209

209

Energia potencjalna

V = -/ty² 2

Korzystając z równań Lagrange’a II rodzaju, napiszemy równanie drgań belki w postaci

|' M +    j + ky = 0    (9.12)

Stąd częstość drgań własnych wynosi

(9.13)

Gdy pominiemy masę belki, częstość ta wyniesie

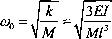
Metoda ta jest prosta i przybliżona. Często się ją stosuje do wyznaczania częstości drgań własnych układów skupionych.

9.3. Układy o wielu stopniach swobody

Wyznaczymy za pomocą współczynników wpływ częstości i postacie drgań głównych jednorodnej belki zamocowanej jednym końcem (rys. 9.3a), obciążonej w punktach ^ =1/3/ i x₂ =1/3/ dwoma masami o ciężarze G. Moment bezwładności przekroju poprzecznego belki -I, moduł sprężystości Younga -E. Masę pominąć (rys. 9.3). Jako współrzędne uogólnione układu przyjmiemy pionowe współrzędne wychylenia ciał od ich położenia równowagi y\ i y%. Celem wyznaczenia współczynników wpływu ó_n, ó_n i $12 wprowadzimy wzory, aby obliczyć ugięcie belki w dowolnym jej przekroju od obciążenia jednostkowego siłą pionową P = 1, przyłożoną w odległości r od zamocowanego końca A belki. Przyjmiemy początek układu współrzędnych o kierunku jak na rys. 9.3b. Równanie różniczkowe linii ugięcia belki ma postać:

(9.14)

d²y

EI^M(x)

ox