Strona0189

189

Z równań Lagrange’a drugiego rodzaju otrzymamy: Il<Pl+K{<Pl -9*2) = 0

(8.39)

(l₂ + r/₃) (p₂ -k_x (ę_x ~<p₂) + ik₂ (i<p₂ -ę_Ą) = 0 ► l₄ęj₄-k₂(i<p₂~ę₄)^0

Pomnóżmy pierwsze z równań (8.39) przez I = I₂+ i^zI₃, drugie zaś przez J_x i odejmijmy je stronami oraz pomnóżmy drugie z równań (8.39) przez I_Ą, trzecie zaś przez 7 i odejmijmy je stronami. Otrzymamy wówczas:

7j7(<p_x -<p_z) + K (h ⁺ ty (^l "<Pi) ~^ifc2^Ji {ⁱ⁽Pz ~ <P4) = ⁰

IJ(ię₂ -ę₄)~ikJ_Ą(ę_x ~ę₂) + k₂(fl_Ą + /)(i(p₂ -<p₄) = 0

Po podzieleniu pierwszego z otrzymanych równań przez //, a drugiego przez 7₄7 otrzymamy:

(8.40)

A + ^anfi ^anp2 ~~ 0

A2 ^2lAl ^22 Aj ®

Układ ma dwa stopnie swobody. Jego współrzędne uogólnione /?, —(pi~<p₂, A = P₂-^4> odpowiednie zaś współczynniki wynoszą:

a,, =

K (/,+/)

ik₂

T

ik_x

T

IJ

Równanie częstości własnych otrzymamy w postaci wyznacznika

a

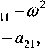
^ai2

^a22 ~^&1

-o

(8.41)

Powyższe równanie można zapisać w postaci o⁴ — (a_n +a₂₂)ó>² 't-a_Mo₂₂ + ci_l2a_2l ⁼ 0