Strona0139

139

Z rozwiązania (6.42) wynika, że w przypadku małego tłumienia drgania swobodne rozpatrywanego układu będą miały postać sumy dwu tłumionych drgań harmonicznych o różnych współczynnikach tłumienia i przesuniętych wzajemnie w fazie.

Zauważmy jeszcze, że w rozwiązaniu ogólnym (6.42) występują tylko cztery stałe dowolne, które możemy wyznaczyć z warunków początkowych (6.44) dlaf«0:

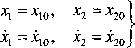
(6.44)

Przy dostatecznie dużym tłumieniu równanie charakterystyczne (6.37) może mieć dwa pierwiastki zespolone sprzężone oraz dwa rzeczywiste:

(6.45)

Ą - -/?j, Ą ~ —, Aj = -h₃ + iw*, A₄ = -h₄ + ico*

przy czym co* jest częstością drgań własnych, a I\, h₄ są liczbami dodat-mmi.

W ogólnym przypadku rozwiązanie ogólne układu (6.32) można zapisać w następującej rzeczywistej postaci:

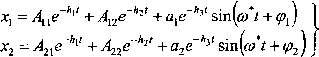
Ruch swobodny układu będzie miał teraz postać ruchu nieokresowego zanikającego, na który nałożą się tłumione drgania harmoniczne. Przy dostatecznie dużym tłumieniu równanie (6.35) może mieć wszystkie cztery pierwiastki X_} (J ~ ł, 2, 3, 4) rzeczywiste ujemne. Wówczas równanie (6.37) jest rzeczywistą postacią rozwiązania ogólnego, a ruch ma charakter nieokresowy zanikający. Częstość drgań własnych tłumionych co\_<2 można wyznaczyć wg wzoru

[&! + k - tr^GJ² + {a_x + a]co\ [fc₂ + k - m₂co² + (a₂ + rz)ey]- (£ + acof = 0

6.4. Drgania wymuszone z tarciem wiskotycznym

Rozpatrzono teraz drgania układu mechanicznego pokazanego na rys. 6.5. Założono, że na masę m_l działa siła p* -P^incot. Równanie dynamiczne zapisano w postaci:

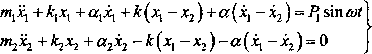
(6.47)