Strona0242

242

Z równania (10.4) wynika, że drgania zanikną, jeżeli 2j + ar₀ >0, co zachodzi na rosnącej części charakterystyki tarcia, gdzie TJ > 0. Przy niedużych wartościach v₀ (opadająca część charakterystyki tarcia) wielkość T₀ jest ujemna (rys. 10.3b). Jeżeli przy tym a₀ >|7j|, to suma + a₀) > 0, drgania są zanikające. Jeżeli suma (7j + ar₀)=0 (tzn. a₀=|7j[), to w równaniu (10.4) zanika człon niesprężystego oporu i możliwe są drgania stacjonarne ze stałą amplitudą. Jeżeli suma (7J + £r₀)< 0, to układ ma „ujemne tłumienie”, tzn. istnieje dopływ energii spowodowany ruchem taśmy i drgania będą narastające. Warunek (7J + ar₀) = 0 zachodzi przy małej prędkości v₀. Wskutek ograniczoności źródła energii drgania samowzbudne w końcu ustalają się (są stacjonarne).

Drgania samowzbudne stacjonarne, pokazane na lys. 10.5, nazwano cyklem granicznym. Cykl graniczny charakteryzuje się tym, że jest niezależny od warunków początkowych. Po zaburzeniu położenia równowagi układ zbliża się do tego cyklu.

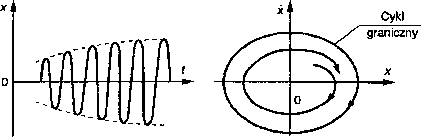
Rys. 10.5

Niekiedy stacjonarne drgania samowzbudne są prawie okresowe i zachodzą z częstością drgań swobodnych układu, wtedy takie układy nazywają się ąuasi--liniowymi. W innych przypadkach stacjonarne drgania znacznie różnią się od harmonicznych, towarzyszą im przystanki i skoki prędkości: takie drgania samowzbudne nazywamy relaksacyjnymi.

10.4. Drgania samowzbudne stacjonarne

Poprzednio siłę tarcia podczas drgań przyjęto za liniowe pr2ybliżenie. Było to wystarczające do badania stateczności położenia równowagi. Analizując proces przejściowy, a także proces ustalony drgań samowzbudnych, musimy uwzględnić człony nieliniowe. Rozłożono siłę tarcia na szereg potęgowy

Av + '

ld ²T

2 dv

(10.5)