078(1)

Znajdźmy pochodną /' i punkty krytyczne, leżące wewnątrz przedziału

[0 ,c]

r- * — |-    -

j/a²+x²    >'V+(x-c)²

x v^/6²+(x-c)^r4- (x—ę) Vc?+x²

>/(a*.+x²)t*²+(*-c)^z]

/' = 0, gdy x j/ó²+(x -^*+(* - c) l/^+JC² = 0

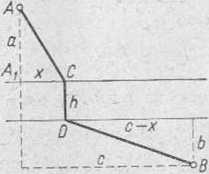
Rys. 64

Rozwiązując to równanie otrzymamy

x¹[b¹Ą-{x-cf] = (x-c)²(a²+x²); b²x² = a\x-cf

ac .    ab

^{Xl =} a^b ¹ X2~a+b

Punkt Xi leży poza przedziałem 0 < x < c; jeśli a > b, to Xi > c, a jeśli a < b, to x_t < 0. Punkt x₂ znajduje się wewnątrz przedziału przy

dowolnych dodatnich wartościach a,b i c, ponieważ wtedy x₂ > 0 i <

< 1, czyli x₂<c.

Pochodna /' istnieje wszędzie; funkcja nie ma więc innych punktów krytycznych.

Wewnątrz przedziału [0, c] funkcja / ma jeden punkt krytyczny, mianowicie x₂. Badając znak pierwszej pochodnej /' na lewo i na prawo od tego punktu, jak to pokazano w tabelce, stwierdzamy, że x₂ jest punktem minimum funkcji.

X	0	Xi	c
/'	-	0	+
1	mai.	min	roś.

Ale zgodnie z własnością / funkcji ciągłych, funkcja ciągła / przybiera w' tym jedynym punkcie minimum w przedziale [0, c] także najmniejszą ze wszystkich swych wartości w tym przedziale.

W konsekwencji, aby długość drogi łączącej dwa obiekty leżące po przeciwnych stronach rzeki była jak najmniejsza, most należy zbudować w takim

QC

miejscu, aby odległość A_XC = yy.

366.    Jaki prostokąt utworzony z kawałka drutu o długości / ma największe pole?

367.    Jeden z boków prostokątnej parceli przylega do brzegu .kanału, a pozostałe trzy boki należy ogrodzić płotem. Jakie powinny być wymiary parceli, aby jej powierzchnia wynosiła 800 m², a długość płotu była jak najmniejsza?

368.    W prostokątnym arkuszu kartonu o długości 48 cm i o szerokości 30 cm wycinamy przy wierzchołkach jednakowe kwadraty, a z pozostałej części sklejamy otwarte pudełko prostokątne. Jakie wymiary powinny mieć boki wyciętych kwadratów, aby pudełko miało największą objętość?

369.    Na prostej łączącej dwa źródła światła o mocy fi 8f znaleźć punkt, który jest najmniej oświetlony, jeżeli odległość obu źródeł wynosi 24 m. (Oświetlenie punktu jest odwrotnie proporcjonalne do jego odległości od źródła światła).

370.    Z danego koła wyciąć taki wycinek, aby po jego zwinięciu powitał stożek o jak największej objętości.

371*. Odległość fabryki A od kolei żelaznej prowadzącej do miasta B wynosi a km, a jej odległość od miasta B wynosi b km. Pod jakim kątem należałoby poprowadzić drogę od fabryki A do kolei, aby dostawa ładunków z A do B kształtowała się jak najtaniej, skoro koszt przewozu drogą jest k razy wyższy niż przewóz koleją?

372.    Cysterna naftowa w kształcie walca zakończonego stożkiem ma być zbudowana na danym fundamencie kołowym i ma mieć narzuconą z góry objętość. Wykazać, że ilość materiału potrzebnego do budowy cysterny będzie najmniejsza wtedy, gdy kąt przy wierzchołku przekroju osiowego

2

stożka będzie równy 2arccos y ^ 96°.

373.    Kanał wodny powinien mieć zadaną głębokość i zadane pole przekroju poprzecznego. Zakładając, że przekrój poprzeczny kanału ma kształt trapezu równoramiennego, obliczyć, jaki powinien być kąt nachylenia ramion trapezu, aby straty na tarcie przy przepływie wody przez kanał były

159