089 3

Równania trygonometryczne)

sin ,v (2 sin⁴* - 3 sin²* + I) = 0 sin * = 0 lub 2 sin⁴* - 3 sin²* +1=0

sin X — 0    Korzystamy z gotowego wzoru.

x = kx, k e C 2 sin⁴* - 3 sin²* +1=0

Wprowadzamy pomocniczą niewiadomą: sin²* = t 2l² - 3/ + I = 0

Otrzymaliśmy równanie kwadratowe, które rozwiązujemy, licząc a i pierwiastki (jeśli a > 0),

A = fc² -4ac = (-3)²- 4 ■ 2 ■ 1 = 9-8 = I

sS = VT= 1

_ -b -'!& _ -(~3) -    1    3-1    ₌2 ₌ I

*'    2 a    2-2    4    4    2

₌ -b+\5 ₌ -(-3) + 1 ₌ 3_+J ₌ 4 ‘² 2a    2-2    4    4

Wracamy teraz do podstawienia:

sin²* = - lub sin²* = 1 2 1

stn-* = —

2

(sin xf = -

Rozwiązujemy teraz dwa równania, niezależnie.

Równanie to ma dwa rozwiązania. Dlatego liczba równań wzrasta.

¹ , , . 1

sin x — —p lub sin x = —p.

'li    'li

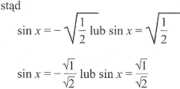
lub sin * =

sin x =

a/2

'li ■'li 'H

'H-'H

89