051

Równania trygonometryczne |

Czyli

2

2x + 1 = - — it + 2kn lub

2

2x + 1 = — it + 2Alt, k e C 3

Teraz rozwiązujemy równanie liniowe, 2

2x + 1 =- — jt + 2Alt /-I

2x = -l -—n + 2kn 1:2 3

Zgodnie ze wzorami redukcyjnymi mamy:

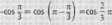
Teraz, pisząc wzory rozwiązań, uwzględniamy fakt, że mamy dany cos (2x + 1). Piszemy dwa równania, które rozwiązujemy ze względu na x, odejmując 1 i dzieląc przez 2.

znaleźć x.

tn

Z-3

2Ait

,    1 JT    ,    ,    _

■ + Kit, czyli x =---- + /ot, k e C

'    2    3

2

2.v + 1 = -it + 2kn h\

2x = -l +    + 2Aa /: 2

3

1    2it 2Ait

2    2-3 ⁺ 2

1 it    1 7t    _

- + - + Kit, czyli x = — — + — + kic, k e C

2 3

Odpowiedź

— ^ + fot lub x = - — + 7 + Au, k e C 2    3    2    3

ZADANIE 13_

Rozwiąż równanie: tgx = 1

Rozwiązanie:

tg x = 1 Za).: x * y+ Alt. A e C

it

4

Jest to równanie elementarne, nie wymaga przekształceń. Znajdujemy taką wartość kąta, dla której tangens przyjmuje wartość 1.

51