1tom210

8. AUTOMATYKA 1 ROBOTYKA

422

wymierną i z łatwością można zastosować kryterium Hurwitza. Kryterium Michaiłów zastosowano dla zilustrowania jego działania. Warunek stabilności otrzymany z ^_rv,^a rium Hurwitza ma postać a, > 2. Zatem przy a_l = 3 układ jest stabilny, a przy a. i a_l=2 — niestabilny. Hodografy wektora M(jco) = H-a₁s+s²+2s²| j = /?(<»)+j/(w), R(to) = 1 —tu², I(o) = a>(a_t—2ar), wyznaczone numerycznie dfa tv_ci, trzech przypadków, potwierdzają to.    ' ¹¹

Zbadano metodą Michajłowa stabilność układu o transmitancji G(s) = 2exp(—3_sv /[exp(—3s)+s(a,+s+2s²)], przy o, = 1, 2 i 3. Wielomian charakterystyczny Afjjcyjil = [cos(3m)—co²] +j[©(a₁—2co²)—sin(3co)]. Warunek Michajłowa jest spełniony jedyni przy a, = 3 (blisko granicy niestabilności) (rys. 8.18b). W pozostałych przypadkach układ jest niestabilny.

Jeżeli wielomian charakterystyczny układu zamkniętego (UZ) nie jest znany, a jest wyznaczona eksperymentalnie charakterystyka a-f układu otwartego (UO), to stabilność można zbadać metodą Nyąuista [8.1; 8.2; 8.6; 8.11; 8.31], Kryterium Nyąuista jest stosowane praktycznie w przypadkach, gdy UO jest stabilny [8.1; 8.2]. W przypadku niestabilności UO, do zbadania stabilności UZ byłaby niezbędna znajomość liczby biegunów UO powodujących tę niestabilność.

Według Nyąuista układ zamknięty o transmitancji G.(s) = G₀(s),/[1 + G₀(s)] jest stabilny, jeżeli charakterystyka a-f układu otwartego G„(jco) nie obejmuje punktu (— 1, jO), tzn. zostawia ten punkt z lewej strony przy zmianie co od 0 do oo. Na przykład URA o transmitancji G„(jtu) = K„exp(—s)/(l + s2,5) jest niestabilny przy K₀ = 4, 5 i 8, a stabilny przy K₀ = 2 (rys. 8.19). Przy K„ = 4, 5 jest na granicy stabilności. Kryterium Nyąuista stosuje się również przy użyciu charakterystyk logarytmicznych [8.1; 8.2; 8.15; 8.31: 8.37]

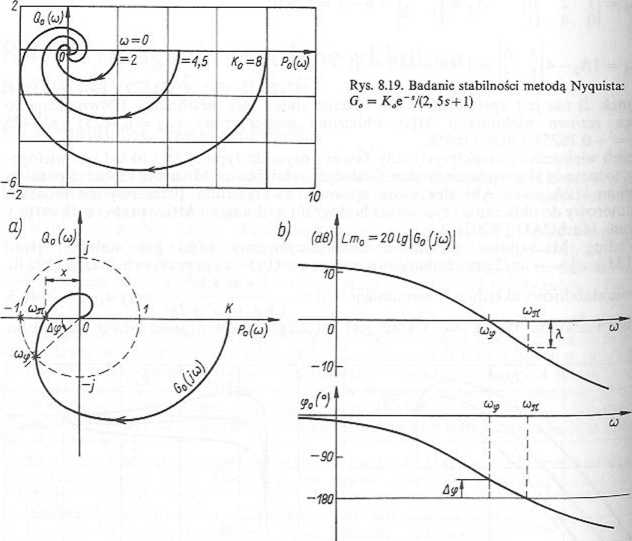
Rys. 8.20. Ilustracja graficzna definicji zapasu stabilności

Badanie stabilności metodą Nyąuista wiąże się z tzw. zapasem stabilności, okreś-• cvin praktyczną przydatność układu zamkniętego [8.15]. Zapas stabilności jest miarą Uległości układu od granicy stabilności. Definiuje się go dla układu zamkniętego na dstawie charakterystyk częstotliwościowych układu otwartego, jako dwójkę liczb r\o) przy czym: /. — zapas modułu, A<p — zapas fazy (w stopniach kątowych); na rys. lonnrzv ż = -201g(.x). Od dobrze zaprojektowanego URA żąda się, by miał dostatecznie duży zapas stabilności, np. większy niż {6 dB, 30°} lub {8 dB, 45°} [8.6; 8.15].

8.4.2. Błędy statyczne i dynamiczne

O niedokładności działania URA świadczą błędy (uchyby) statyczne i dynamiczne. Uchyb /₍) _ma dwa składniki: uchyb nadążania e_w(t) i uchyb tłumienia zakłóceń e_z(t) [8.1]. W liniowym URA składniki te sumują się. W stanie statycznym, tj. w stanie ustalonym przy wymuszeniu skokowym o amplitudzie A, statyczny błąd. reputacji

co) = hm lsH_e(sj]

s=> 0

lim

= e(t--

s — G.(s)"| = lim UG.(s)]    (8.27)

J 5=>0

przy czym: H_e — transformata Laplace’a charakterystyki skokowej; G_e = 1/[1 + GJ dla sygnału w(t), a G_e = GJ\ + G„] dla zakłócenia; G_a — transmitancja układu otwartego: G — transmitancja ” zakłóceniowa. Stad uchyb statyczny e_s = e_s„+e_sz = [A„+

Jeżeli e_s = 0, to URA jest nazywany astatycznym. Układ jest astatyczny, jeżeli w R(s) lub G„(s) występuje człon całkujący. W statycznym URA uchyby statyczne e„ = AJ\_ 1 + K_rK_oh], e_sz = A_SKJ\_ 1 +K_rK_ob], przy czym: K_r, K_ob i K₂ — wzmocnienia regulatora, obiektu i toru zakłócenia.

Uchyby dynamiczne e(t) są związane ze stanami dynamicznymi URA. Dokładność dynamiczną URA określa się za pomocą uchybów w stanach ustalonych przy wymuszeniach standardowych typu skok prędkości    skok przyspieszenia a₀t²l(t) lub fala

harmoniczna a_Acos(o>£) l(t). Uchyby dynamiczne związane z tymi sygnałami (prędkoś-ciowy, przyspieszony i częstotliwościowy) wynoszą

«.*=». lim [d [G_c(s)]/ds],

$=>0

^ehW = Ufc|G_c0'm)l

= a„ lim [d²[G_s(s)]/ds²]/2

(8.28)

Uchyb e_v jest równy zeru w układzie astatycznym drugiego rzędu, ae₍ — w układzie astatycznym trzeciego rzędu, tj. w URA zawierającym odpowiednio co najmniej 2 i 3 człony całkujące.

8-4.3. Kryteria oceny jakości układów regulacji automatycznej

Jakość URA ocenia się na podstawie całego przebiegu przejściowego e(t)Vte[0,co], " cpju wyeliminowania subiektywizmu oceny wprowadza się miary jakości przebiegu Przejściowego e(t) — tzw. wskaźniki jakości regulacji. Najpopularniejszymi wskaźnikami jakości regulacji są [8.1; 8.2; 8.6; 8.9; 8.15; 8.30; 8.31]:

> uchyby: statyczny, prędkościowy, przyspieszony częstotliwościowy i maksymalny ^em ~ max[e(t)] (rys. 8.21);

k) czas regulacji ^rozumiany jako czas po jakim |e(t)| < A V(_r > i, gdzie A — dopuszczalne odchylenie przyjmowane jako (5% lub 1%) e_m albo (1% lub 5%) amplitudy

, wymuszenia;

, Pr^eregulowanie * = 100AJA₀ i oscvlacyjność d = 100^4₂Mi, ^w procentach;

' wskaźniki całkowe: IAE = /[|e(t)|], IŚE = J[e²(t)],ITAE = I[t|e|] i ITSE = I[te²(t)l

CC

gdzie operator /[...] = j [,..]d£.

ś_cj j^ujczęściej dąży się do zaprojektowania regulatora tak, by wybrany wskaźnik jako-’ P- JAE lub t_r, był minimalny przy dostatecznie d użym zapasie stabilności [8.15; 8.30].