1tom212

8. AUTOMATYKA I ROBOTYKA

-426

Logarytmiczna charakterystyka fazy takiego układu otwartego jest symetryczna w dem pulsacji co_g = (7j T₂)~ ¹ . Symetrię charakterystyki logarytmicznej modułu uk^Jf otwartego osiąga się, nastawiając wzmocnienie K = I /(7j _v T, T₂). Zapas fazy w y zaprojektowanym URA zależy od ilorazu a = TJT₂. Przy z = 4, 8" 10, 20 i 50 zanas r Acp wynosi odpowiednio: 37^c, 51^c, 55°, 65° i 74°, a M_p wynosi: 1,682, 1,33, 1,275 1 pi i 1,105. Wartość M_p można zmniejszyć przez nieznaczne zwiększenie wzmocnienia'

Przy projektowaniu kaskadowych URA najpierw dobiera się regulator wewnętrzny Po jego nastawieniu dobiera się regulator zewnętrzny. Tłumienie zakłóceń w kaskadowym URA jest ok. 20 razy większe niż w jednoobwodowym URA.

Regulator impulsowy można dobrać tak, by do stanu statycznego dochodził w skończonym czasie t = pT_s [8.1; 8.4], Tak reagujący regulator na skok sygnału w(t) powinien mieć transmitancję impulsową R(z) = jVf₀(z)/[L„(l)z^,’-I₀(z)], obliczaną na podstawie transmitancji impulsowej obiektu z ekstrapolatorem G„(z) = i₀(z)/Af_o(z),

G₀{z) = ^[^-'[(1 -c-*^T-)GJs)M,-kTrI

przy czym G_ob(s) — transmitancja obiektu (ciągłego) rzędu n₀; T — okres impulsowania: p 3= n₀; 2C i Sć — przekształcenia operatorowe Laurenta i Laplace’a [8.1].

Prawo sterowania regulatora impulsowego w postaci wzoru rekurencyjnego wyznacza się na podstawie transmitancji R(z) = L_r(z)/Af_r(z)

= lg_mre(k + mr-nr) + g_m,-_le(k + mr + nr-l)+ ... +g₀e(k-nr)]~

- Om- -1 u(k -1)+h_nr _ 2 u(k - 2)+ ... + h₂ u(k - nr +1)+h₀u(k - nr)]/h„, przy czym g-, i h_::

mr    nr

L_r(z) = X Gi^z‘; Af,(z) = £ h,ć

i = O    i = O

Przy p = n„, URA osiąga stan ustalony n₀ krokami (impulsowaniami). Jeśli w celu zmniejszenia czasu regulacji skróci się 7], to wzrośnie max(|u(k)|) i po osiągnięciu nasycenia urządzenia wykonawczego czas regulacji przestanie maleć, ponieważ samorzutnie zwiększy się liczba kroków.

8.5. Nieliniowe układy regulacji automatycznej

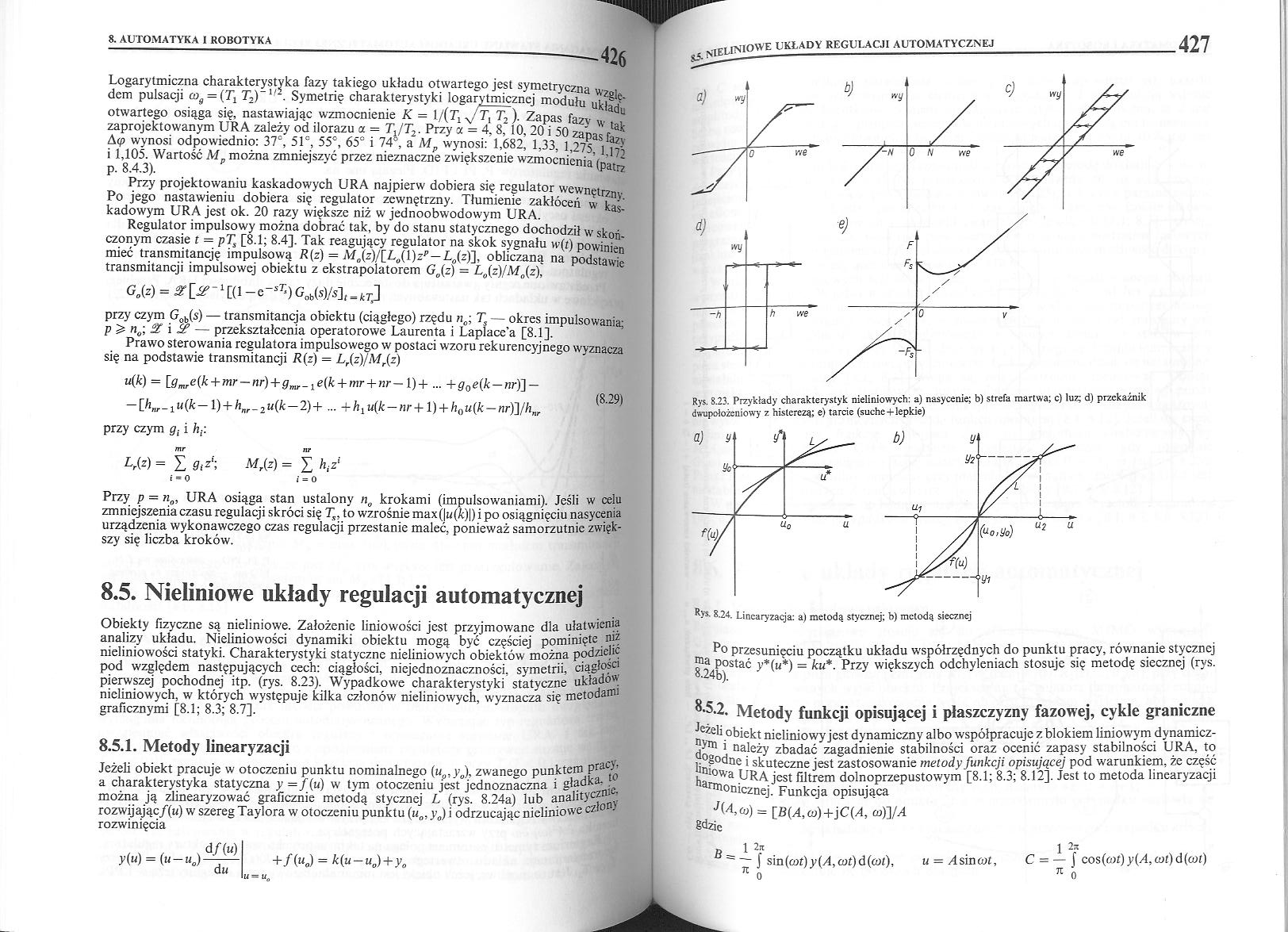
Obiekty fizyczne są nieliniowe. Założenie liniowości jest przyjmowane dla ułatwieniu analizy układu. Nieliniowości dynamiki obiektu mogą być częściej pominięte niz nieliniowości statyki. Charakterystyki statyczne nieliniowych obiektów można pod/jcuę pod względem następujących cech: ciągłości, niejednoznaczności, symetrii, ciąg^sci pierwszej pochodnej itp. (rys. 8.23). Wypadkowe charakterystyki statyczne układ®, nieliniowych, w których występuje kilka członów nieliniowych, wyznacza się metoda graficznymi [8.1; 8.3; 8.7].

8.5.1. Metody linearyzacji

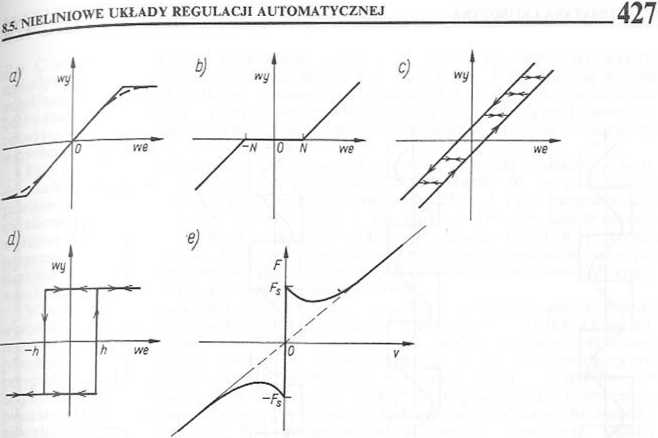
Jeżeli obiekt pracuje w otoczeniu punktu nominalnego (u_p,y„), zwanego punkteni a charakterystyka statyczna y = f(u) w tym otoczeniu jest jednoznaczna i gł?dkiu można ją zlinearyzować graficznie metodą stycznej L (rys. 8.24a) lub anality^c rozwijającf(u) w szereg Taylora w otoczeniu punktu (u„, y₀) i odrzucając nieliniowa cz rozwinięcia

df(u)

du

+/(«„) = k(u-u₀)+y„

y(u) = (u-u₀)

Po przesunięciu początku układu współrzędnych do punktu pracy, równanie stycznej Postać y*(u*) = ku*. Przy większych odchyleniach stosuje się metodę siecznej (rys. °.24b).

8-5.2. Metody funkcji opisującej i płaszczyzny fazowej, cykle graniczne

^żeli obiekt nieliniowy jest dynamiczny albo współpracuje z blokiem liniowym dynamicz-do \ ^należ>' zbadać zagadnienie stabilności oraz ocenić zapasy stabilności URA, to _y2°dnc i skuteczne jest zastosowanie metody funkcji opisującej pod warunkiem, że część harrn"^{1 2 3} jest filtrem dolnoprzepustowym [8.1; 8.3; 8.12]. Jest to metoda linearyzacji 'fonicznej. Funkcja opisująca

^JU,(o) = [B(A,o)+iC(A, co)]/A gdzie

1 2*

J s i n (eof) y (/I, o t) d (ca /),    u = Asinwf,

Rys. S.23. Przykłady charaktery⁵¹)* nieliniowych: a) nasycenie; b) strefa martwa; c) luz; d) przekaźnik dwupoloźeuiowy z histcrezą; e) tarcie (suche+lepkie)

1

2

C = — J cos(t»f) y(A,<ot)d(a)t)

3

^K o