216 217

216 Metody wielokryterialne

Formułujemy zadanie Z_m i zadanie Z,₎₂, rozpatrując kolejno występujące w zadaniu wielokryterialnym funkcje celu. Otrzymujemy:

216 Metody wielokryterialne

Zadanie Zq,

2x, + 3x₂ —> max, ar, + 2x₂ < 8,

4x,    < 16,

x_h x₂^0.

Zadanie Z>2

— 2jC| — 3x₂ —> max,

+ 2x₂ < 8,

4jC| ^ 16, i_h x₂ > 0.

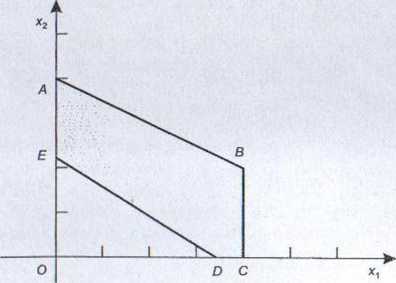
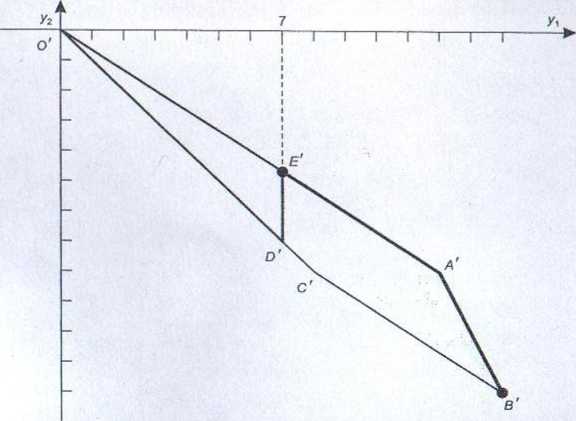
Wspólny dla obu zadań zbiór rozwiązań dopuszczalnych w przestrzeni decyzyjnej przedstawiono na rys. 4.1. Rozwiązaniem optymalnym R_ol zadania Z,| w przestrzeni kryterialnej jest punkt B\ natomiast rozwiązaniem optymalnym R_m zadania Zo₂ w przestrzeni kryterialnej jest punkt O' (rys. 4.3).

Wartości kryteriów /, i f₂ dla rozwiązań /?<„ i R_a2 zestawiono w tablicy 4.5.

Jeżeli decydent uzna, że jako rozwiązanie końcowe może wybrać rozwiązanie R_t)l (czyli punkt B'), stwierdza w ten sposób, że w swoim wyborze kieruje się zdecydowanie wartościami pierwszego kryterium, które ma dla niego znaczenie priorytetowe. Jeżeli decydent uzna, że jako rozwiązanie końcowe należy wybrać rozwiązanie R₍₎₂ (czyli punkt O'), to tym samym stwierdza, że w swoim wyborze kieruje się wyłącznie wartościami drugiego kryterium, które ma dla niego największe znaczenie. W przypadku wyboru jako rozwiązania końcowego innego rozwiązania niezdominowanego decydent uznaje, że jest skłonny zaakceptować kompromis między wartościami rozpatrywanych kryteriów. Kompromis ten określa jednocześnie jego preferencje względem rozpatrywanych kryteriów.

Na podstawie tablicy 4.5 można stwierdzić, że najlepsza aktualnie wartość dla kryterium/,, czyli wartość optymistyczna, to 14, a najlepsza wartość dla kryterium f₂ to 0. Aktualne wartości akceptowane są równe odpowiednio 0 oraz — 12. Wartości te przedstawiono w tablicy 4.6.

Tablica 4.5

^\Kryterium
Wartość \	/l	fl
*0.	14	-12
*02	0	0

Tablica 4.6

" ^ Kryterium	/.	fi
Wartość
Akceptowana	0	-12
Optymistyczna	14	0

Przypuśćmy teraz, że decydent nie jest skłonny do rozpatrywania rozwiązań, w których wartość /, jest mniejsza od 7. Jednocześnie nie może dopuścić do tego, aby wartości kryterium /₂ były mniejsze od wartości akceptowanej dla tego kryterium. Powstają w ten sposób dwa nowe zadania jednokryterialne: Z,, i Z_l2, w' których dołączamy dwa dodatkowe warunki ograniczające, omówione powyżej. Zadania te mają postać:

r

217

Generowanie rozwiązań sprawnych

Zadanie Z,,

2x,+3x₂ -> max, *, +2x₂ <8,

4x,    < 16,

2x₁ + 3x₂ S* 7,

-2x,-2*₂>- 12,

X|> x₂ ^ 0.

Zadanie Z,₂

— 2x, -2x₂ —» max,

+2x₂ < 8,

4xi < 16,

2x, +3x₂ > 7, -2x, -2jc₂ > — 12, X|, x₂ > 0.

Rysunek 4.14

Rysunek 4.15