288 289

6.1. Wprowadzenie

W poprzednich rozdziałach rozpatrywaliśmy zadania, w których zarówno funkcja celu, jak i wszystkie warunki ograniczające były liniowe. Okazuje się, że model liniowy jest rzeczywiście ujęciem najczęściej wykorzystywanym w modelowaniu wielu zagadnień z zakresu ekonomii i zarządzania, a także z wielu innych dziedzin. Możliwość wykorzystania efektywnych algorytmów, w szczególności metody simpleks, powoduje, że programowanie liniowe bywa stosowane również w tych sytuacjach, gdy założenia dotyczące liniowości funkcji celu i warunków ograniczających spełnione są tylko z pewnym przybliżeniem. Często jednak charakter funkcji celu lub warunków ograniczających tak bardzo odbiega od liniowości, iż zastosowanie modelu liniowego jest całkowicie nieuzasadnione. Dlatego też powstało wiele metod rozwiązywania zadań, w których funkcja celu lub przynajmniej jeden warunek ograniczający nie jest liniowy. Zadania te, nazywane zadaniami programowania nieliniowego, stanowią bardzo obszerną klasę zadań.

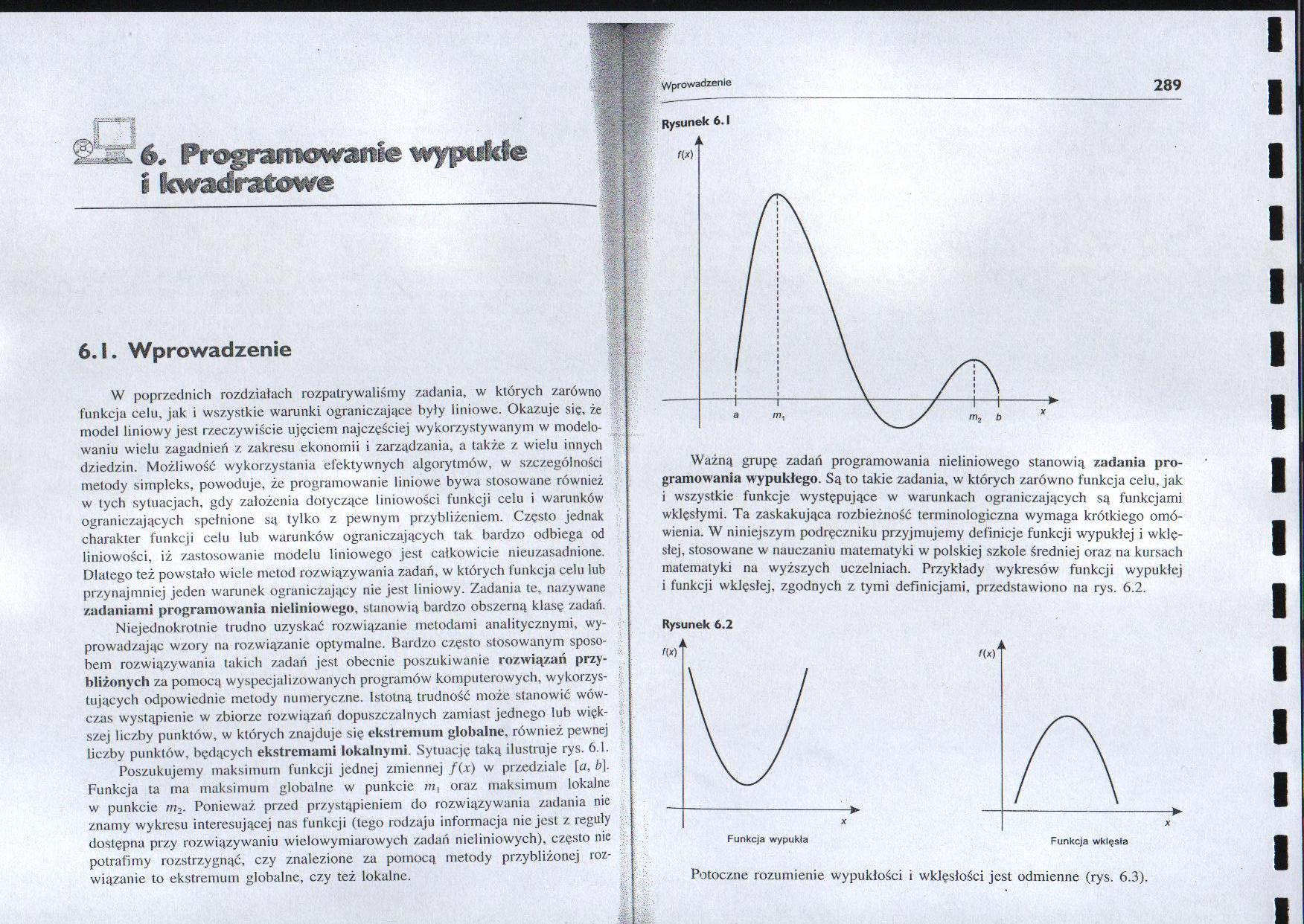
Niejednokrotnie trudno uzyskać rozwiązanie metodami analitycznymi, wyprowadzając wzory na rozwiązanie optymalne. Bardzo często stosowanym sposobem rozwiązywania takich zadań jest obecnie poszukiwanie rozwiązań przybliżonych za pomocą wyspecjalizowanych programów komputerowych, wykorzystujących odpowiednie metody numeryczne. Istotną trudność może stanowić wówczas wystąpienie w zbiorze rozwiązań dopuszczalnych zamiast jednego lub większej liczby punktów, w których znajduje się ekstremum globalne, również pewnej liczby punktów, będących ekstremami lokalnymi. Sytuację taką ilustruje rys. 6.1.

Poszukujemy maksimum funkcji jednej zmiennej f(x) w przedziale fa, b\. Funkcja ta ma maksimum globalne w punkcie m, oraz maksimum lokalne w punkcie m₂- Ponieważ przed przystąpieniem do rozwiązywania zadania nie znamy wykresu interesującej nas funkcji (tego rodzaju informacja nic jest z reguły dostępna przy rozwiązywaniu wielowymiarowych zadań nieliniowych), często nie potrafimy rozstrzygnąć, czy znalezione za pomocą metody przybliżonej rozwiązanie to ekstremum globalne, czy też lokalne.

Rysunek 6.1

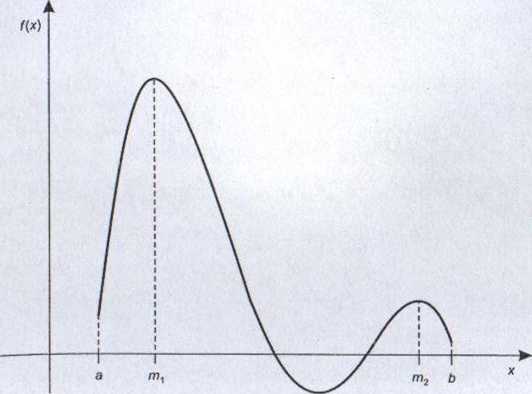
Ważną grupę zadań programowania nieliniowego stanowią zadania programowania wypukłego. Są to takie zadania, w których zarówno funkcja celu, jak i wszystkie funkcje występujące w warunkach ograniczających są funkcjami wklęsłymi. Ta zaskakująca rozbieżność terminologiczna wymaga krótkiego omówienia. W niniejszym podręczniku przyjmujemy definicje funkcji wypukłej i wklęsłej, stosowane w nauczaniu matematyki w polskiej szkole średniej oraz na kursach matematyki na wyższych uczelniach. Przykłady wykresów funkcji wypukłej i funkcji wklęsłej, zgodnych z tymi definicjami, przedstawiono na rys. 6.2.

Rysunek 6.2

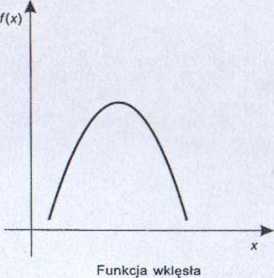
Potoczne rozumienie wypukłości i wklęsłości jest odmienne (rys. 6.3).