296 297

296 Programowanie wypukłe i kwadratowe

Ponadto mówimy, że spełniony jest warunek Slatera, jeżeli w zbiórce rozwiązań dopuszczalnych istnieje taki punkt x*, że dla każdej funkcji g„ która nie jest liniowa, zachodzi g,(x*)>0. Warunek ten spełniony jest we wszystkich rozpatrywanych dalej problemach.

Rozwiązaniem problemu Kuhna-Tuckera jest taki wektor (x°, y°), że spełnione są jednocześnie warunki 1-4 i warunek Slatera.

Istotne znaczenie dla rozwiązywania zadań programowania wypukłego ma przytoczone poniżej twierdzenie Kuhna-Tuckera.

Twierdzenie 6.3

Problem programowania wypukłego i problem Kuhna-Tuckera są sobie równoważne.

Z powyższego twierdzenia wynika, że zamiast rozwiązywać problem programowania wypukłego, można skonstruować odpowiadający mu problem Kuhna--Tuckera. Jego rozwiązaniem jest para wektorów (x°, y°). Otrzymany wektor x° jest jednocześnie rozwiązaniem wyjściowego problemu programowania wypukłego.

6.2.4. Wykorzystanie warunków Kuhna-Tuckera do rozwiązywania zadań programowania wypukłego

Rozwiązanie problemu Kuhna-Tuckera może być bezpośrednio wykorzystywane do rozwiązania problemu programowania wypukłego. W celu zilustrowania tej możliwości rozpatrzymy ponownie zadanie z przykładu 6.1. Tworzymy funkcję Lagrange’a i obliczamy pochodne cząstkowe względem x₂- Mamy:

L(xi, x₂, y„ y₂, y₃) = x, + x₂+y_l(8-xl-xj)+y₂x_] + y₂x₂,

dL , „

— = 1 —2 y,x,+y₂,

(./X |

3L , „

—= 1-2 y,x₂+y_v 0X2

Układ warunków Kuhna-Tuckera zapisujemy następująco:

• warunek 1:

dL

— = 1 -2y,.*| +y₂ = 0,

|^=l-2y,x₂ + y, = 0.

CJX 2

•    warunek 2:

.V! (8 - x f - x\) + y₂ x, + y₂x₂ = 0.

•    warunek 3:

g_l(x) = S-x^-xj^0, g₂{x)-x| >0,

£₃tr) = *₂2s0.

•    warunek 4:

yi >0,    > 0, y₃ ^ 0.

Warunek 2 jest sumą trzech składników, z których każdy jest iloczynem dwóch nieujemnych czynników. Jeżeli taka suma jest równa zeru, oznacza to, że każdy ze składników jest równy zeru, czyli y,(8-;c^{1 2}-.r₂) = 0, y₂-^ri=0 i y_}x₂ = o.

Zbiór rozwiązań dopuszczalnych, określony przez warunki g, ^ 0, g₂ > 0, g₃^0 i przedstawiony graficznie na rys. 6.6, dzielimy na podzbiory następująco²:

Podzbiór 1

Wszystkie warunki są spełnione jako ostre nierówności, czyli:

giC*i. -*2) > o, g₂(x,, .r₂) > 0, gj(jc„ x₂) > 0.

Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki przedstawiono na rys. 6.6. Jest to wnętrze wycinka koła OAB. Linia przerywana wskazuje na to, że punkty brzegowe nie należą do rozpatrywanego zbioru.

Rysunek 6.6    Rysunek 6.7

1

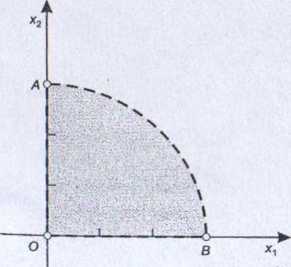
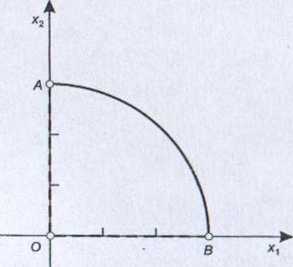
Idea podziału zbioru rozwiązań dopuszczalnych na podzbiory i poszukiwanie w nich punktów

2

spełniających warunki Kuhna-Tuckera zostały zaczerpnięte z pracy W. Grabowskiego, Programowanie matematyczne, PWE, Warszawa 1980.