310 311

310

Programowanie wypukłe i kwadratowe

Tablica 6.6

cx —	min	0	0	0	0	0	0	0	0	1	1	1	b
Baza	Cb	*1	*2	r<! ^x l	*2	yi		Si	yi	V|	w,	Wj
*2	0	0.5	1	0,5	0	0	0	0	0	0	0	0	5
V|	0	1,5	0	-0,5	0	i	-0,5	0	-0,5	0	0	0,5	7,5
Sl	0	-16,5	0	1.5	0	0	0,5	1	-0,5	0	-1	0,5	17,5
V,	1	0,5	0	-0,5	-1	0	0	0	0	1	0	0	4
Cj-	“ Zj	-0,5	0	0,5	1	0	0	0	0	0	1	1	X

Iteracja 5

Jedyną zmienną z ujemną wartością współczynnika optymalności, kandydującą do wejścia do bazy jest *,. W bazie znajduje się jednak zmienna y‘! komplementarna do jc, i jej wyeliminowanie nie jest możliwe. W bazie pozostała jeszcze zmienna sztuczna v, i jej wartość jest dodatnia. Sytuacja taka nie wskazuje jednak na to, że rozpatrywane zadanie jest sprzeczne, gdyż — jak łatwo się przekonać geometrycznie — zbiór rozwiązań dopuszczalnych zadania wyjściowego nie jest pusty. Zwróćmy uwagę na to, że do bazy można wprowadzić zmienne niebazowe, które mają współczynnik optymalności równy 0. Taką zmienną jest w rozpatrywanej iteracji zmienna y₂. Po jej wprowadzeniu do bazy okazuje się, że bazę opuszcza zmienna y'j (tablica 6.7).

Tablica 6.7

cx —)	min	0	0	0	0	0	0	0	0	1	1	1
baza	Cl.	*1	*2	yi!	xi	y<	y2	Si	yi	V|		W2
*2	0	0,5	1	0,5	0	0	0	0	0	0	0	0	5
.Vi	0	-15	0	1	0	i	0	t	-1	0	-1	1	25
yi	0	-33	0	3	0	0	i	2	-1	0	-2	1	35
V,	1	0,5	0	-0,5	-1	0	0	0	0	1	0	0	4
<7-	'Z;	-0,5	0	0,5	1	0	0	0	0	0	1	1	X

Iteracja 6

W iteracji 6 wartości współczynników optymalności nie zmieniają się w stosunku do iteracji 5, ponownie więc chcemy wprowadzić do bazy zmienną*,. Jest to teraz możliwe, gdyż zmienna y‘l komplementarna do *, nie jest już zmienną bazową.

Iteracja 7

Na początku iteracji 7 otrzymujemy tablicę 6.8.

Tablica 6.8

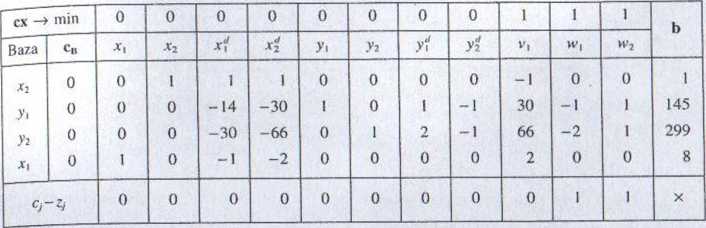
Ponieważ wszystkie współczynniki optymalności są nicdodatnie, otrzymane rozwiązanie jest rozwiązaniem optymalnym zadania zastępczego. Optymalna wartość funkcji celu w zadaniu zastępczym wynosi 0. Odczytujemy rozwiązanie zadania wyjściowego, które jest następujące:

x, = 8, x₂ = 1 ■

Optymalna wartość funkcji celu zadania wyjściowego jest równa -568.

Przykład 6.4

Rozpatrujemy zadanie:

/(*,, x₂)= 10x| —25j:₂— 10xf — jcj — 4x,x₂ -> max, x, + 2x₂    10,

-x_t-x₂ <-9, r, >0,

*2 > 0.

Powyższe zadanie różni się od zadania 6.3 wartością jednego współczynnika funkcji celu, mamy bowiem p₂<0. Ponownie zapisujemy funkcję Lagrange’a, warunki Kuhna-Tuckera i zadanie zastępcze, które przyjmuje postać:

Vi + vy, —> min, x_[ + 2x₁+x‘{= 10, x_i+x₂-x₂ + v_l =9,

20x.+4jc₂+y,-y₂-yf-MV| = 10,

— 4x | — 2x₂ — 2y | + y₂ + y ₂ ~ 25,

*1. x₂, xi, xi, y_u y₂, yi, yi, v,, w, Ss 0.