320 321

320 Programowanie wypukłe i kwadratowe

Funkcje celu:

• minimalizacja ryzyka portfela:

11,4312	1,1701	0,1232	1,6619	2,0254
1,1701	7,7723	0,4983	1,1374	1.7056
0,1232	0,4983	5.1598	-1,3094	-0,6307
1,6619	1,1374	- 1,3094	20,2858	2,2824
2,0254	1,7056	-0,6307	2,2824	4,3189

• maksymalizacja oczekiwanej stopy zysku portfela: 0.94.r, + 1,20x₂-0,02xy¥0,81 x₄+ 0,45 x₅ —> max.

Warunki ograniczające:

•    udziały akcji w portfelu sumują się do jedności: x, + x₂+x₃+x₄+x₅ = 1,

•    warunki nieujemności:

x,, x₂, x₃, x₄, x₅ > 0.

Rozwiązanie optymalne

Chcąc znaleźć rozwiązania optymalne wektorowo, zastosujemy metodę satysfakcjonującego poziomu kryteriów opisaną w podrozdziale 4.4.2. Będziemy minimalizować pierwszą funkcję celu, przyjmując różne poziomy oczekiwanego zysku portfela. Rozwiążemy ciąg następujących zadań w postaci przystosowanej do wykorzystania programu KWADRAT.EXE:

- [.*•, x₂ x, x₄ jt₅]

11,4312	1,1701	0,1232	1,6619	2,0254
1,1701	7,7723	0,4983	1,1374	1,7056
0,1232	0,4983	5,1598	- 1,3094	-0,6307
1,6619	1.1374	- 1,3094	20.2858	2.2824
2,0254	1,7056	-0.6307	2,2824	4,3189

[.<■, x₂ xj x_A jc_s)^t —> max.

przy warunkach ograniczających:

- 0,94x, - 1,20 x₂ + 0,02x, - 0,81 x₄ - 0,45 x₅    - r₀,

X|+X₂ +x₃ + x₄ + x₅ < 1,

—x, — x₂ — x₃ — x₄ — x₅    1,

X|, x₂, x₃, x₄, x₅ > 0.

Wykonamy obliczenia dla wartości r₀, wyszczególnionych w tablicy 6.13, w której zamieszczamy również wyniki obliczeń. Widzimy, że obniżając poziom oczekiwanego zysku, otrzymujemy portfele o coraz mniejszym ryzyku. Portfele przedstawione w tablicy 6.13 to przykładowe rozwiązania sprawne dwukryterial-ncgo zadania poszukiwania optymalnego portfela akcji. Wszystkich sprawnych portfeli jest nieskończenie wiele.

Tablica 6.13

Portfel	Parametry portfeli wyznaczonych dla założonych wartości r„
	r<>	*V	X,	*2		-*4	*5
p,	1,2	2,79	0	1	0	0	0
Pi	1,15	2,42	0,1841	0,8104	0	0,0054	0
p>	1,1	2,20	0.2527	0,6594	0	0,0879	0
p&	1.0	2,00	0,2468	0,5391	0,0285	0,1060	0,0797
Pf,	0,9	1,83	0,2171	0,4671	0,0897	0,0986	0,1275
p„	0,8	1,67	0,1874	0,3951	0,1510	0,0911	0,1754
p-,	0,7	1,53	0,1577	0,3231	0,2122	0,0837	0,2233
p»	0,6	1.43	0,1280	0,2511	0.2734	0,0763	0,2711
p.	0,5	1,36	0,0984	0,179!	0,3347	0,0689	0,3190
P10	0.4	1.34	0,0687	0,1071	0,3959	0,0615	0,3668

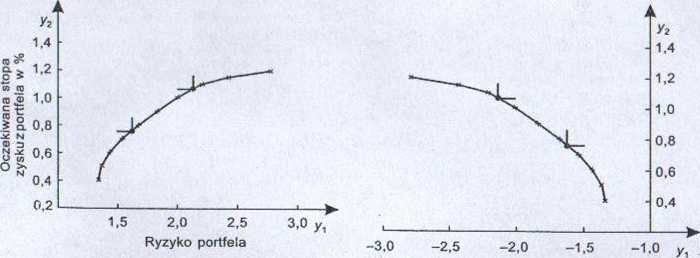
Wyniki obliczeń przedstawimy graficznie w przestrzeni kryterialnej. Oś Oy, przedstawia ryzyko portfela, a oś Oy₂ — oczekiwaną stopę zysku portfela. Łącząc ze sobą wyznaczone punkty, otrzymujemy linię, która w teorii portfela nosi nazwę granicy efektywnej. Jest to zbiór rozwiązań niczdominowanych zadania dwu-kryterialnego w przestrzeni kryterialnej (rys. 6.13).

Rysunek 6.13    Rysunek 6.14