298 299

Programowanie wypukłe i kwadratowe

298

Podzbiór 2

Pierwszy warunek jest spełniony jako równość, pozostałe zaś jako ostre nierówności, czyli:

£,(^{1 2}„ ²₂) = 0, g2(²H²2)>0, gjOct, x₂) > 0.

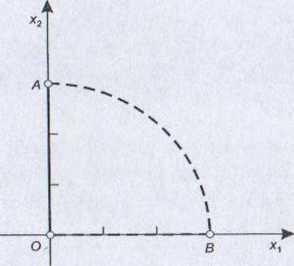
Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki ilustruje rys. 6.7. Jest to luk wyznaczony przez punkty A i B okręgu, bez tych punktów.

Podzbiór 3

Rysunek 6.8

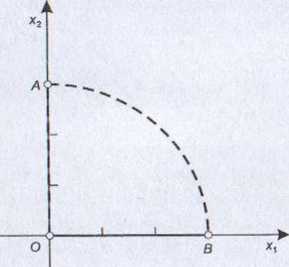
Rysunek 6.9

Podzbiór 4

Trzeci warunek jest spełniony jako równość, pozostałe zaś jako ostre nierówności, czyli:

«,(²„ -²2) >0, g₂(.x„ x₂)>0, g₃(x„ x₂)=0.

Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki przedstawiono na rys. 6.9. Są to punkty leżące na odcinku OB, z wyłączeniem jego końców.

Podzbiór 5

Pierwszy i drugi warunek są spełnione jako równości, trzeci jako ostra nierówność, czyli:

g,(²i, ²₂)=0, g2(x„ x₂)=0, g₃(x„x₂)> 0.

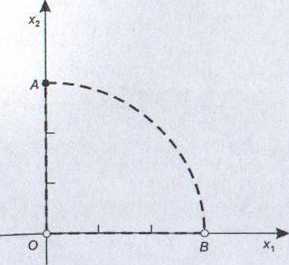
Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki ilustruje rys. 6.10. Jedynym elementem tego zbioru jest punkt A.

Rysunek 6.10    Rysunek 6.1 I

Podzbiór 6

Pierwszy i trzeci warunek są spełnione jako równości, a drugi jako ostra nierówność, czyli:

gi(*i. -t₂) = 0, g₂(*i, x₂) > 0, £.,(*„ *₂) = 0.

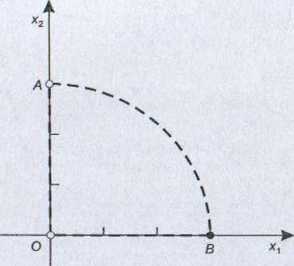
Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki przedstawiono na rys. 6.11. Jedynym elementem tego zbioru jest punkt B.

Podzbiór 7

1

Drugi warunek jest spełniony jako równość, pozostałe jako ostre nierówności, czyli:

2

2) > 0, £₂(²i, ²2) = 0, £,(²„ ²₂) > 0.

Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki przedstawiono na rys. 6.8. Są to punkty leżące na odcinku OA z wyłączeniem jego końców.

Drugi i trzeci warunek są spełnione jako równości, a pierwszy jako ostra nierówność, czyli:

gi(*i> *2) >0, g₂(x„x₂) = 0, g₃(x„x₂) = 0.

Zbiór punktów płaszczyzny spełniających wszystkie powyższe warunki ilustruje rys. 6.12. Jedynym elementem tego zbioru jest punkt O.

Podzbiór 8

Wszystkie warunki są spełnione jako równości, czyli:

Si(*i, *₂) = 0, g₂(Jc„ *₂) = 0, g₃(*o x₂) = 0.

Podzbiór 8 jest zbiorem pustym.

Sposób tworzenia podzbiorów wskazuje na to, że są one rozłączne, a ich suma mnogościowa to cały zbiór rozwiązań dopuszczalnych.

Zbadamy teraz, czy w kolejnych podzbiorach istnieją punkty spełniające warunki Kuhna-Tuckera.