2tom244

6. NAPĘD ELEKTRYCZNY 490

statyczna odpowiada stosunkowi 0_sN:0_b k 2. Przy biegu jałowym, gdy i_a = 0 silnik osiąga ograniczoną prędkość

Q₀ —

1,5 Q_n

Silnik taki łączy cechy silnika szeregowego i bocznikowego, gdyż rozwija (dzięki uzwojeniu szeregowemu) znaczne momenty, np. w czasie rozruchu, ograniczając prędkości biegu jałowego (dzięki przepływowi magnetycznemu od uzwojenia bocznikowego).

Zależność wypadkowego strumienia w szczelinie od prądu twornika decyduje o nieliniowości równań opisujących stany silnika szeregowo-bocznikowego. Należy więc analizę jego stanów statycznych i dynamicznych prowadzić tak jak dla silnika szeregowego, posługując się charakterystykami katalogowymi oraz metodą małych przyrostów wokół punktu pracy.

6.2.3. Silniki indukcyjne trójfazowe

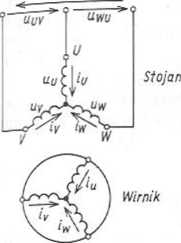
Silniki te znajdują coraz szersze zastosowanie ze względu na swoje zalety, takie jak prostota konstrukcji oraz związana z tym taniość i pewność działania. Możliwość budowy silników o dużych mocach i szerokich zakresach prędkości obrotowych pozwala na realizację napędów z bezpośrednim sprzężeniem silnika oraz maszyny roboczej, z pominięciem kosztownej przekładni mechanicznej. Z uwagi na wiele wspólnych cech, można silniki pierścieniowe oraz klatkowe analizować za pomocą wspólnego modelu, podkreślając występujące odrębności, jakie wykazują zwykle silniki zwarte głębokożłobkowe czy dwuklatkowe. Zakładając zarówno symetryczną budowę obwodu magnetycznego oraz uzwojeń stojanai wirnika, jak też i monoharmoniczność pola magnetycznego w szczelinie między stojanem a wirnikiem, można zgodnie z oznaczeniami na rys. 6.31 zapisać równanie równowagi obwodów elektrycznych (prądy i napięcia oraz rezystancje i im-pedancje wirnika zostały sprowadzone do obwodu uzwojenia stojana)

u_v= ^Ruh+

*y — l\y ly '

d^	uu = Ru	dW f +—-
dt		" dt
d<?V b--	uv = Rv	. d*P„
dr		' ' dt
]	«... = R..	d'F„ . i... H--—

dt

dt

(6.66)

W maszynie symetrycznej rezystancje fazowe są sobie równe: R_v = R_v = R_w = R_s oraz R„ = R_v = £„• = R_r- Strumienie W_v, t'_v i W_w, jak również V_u, f'_L. i są odpowiednio całkowitymi strumieniami sprzężonymi z pasmami (fazami) U, V, W uzwojenia stojana zaś u, v, w — uzwojenia wirnika. Wprowadzając wektory przestrzenne, szczególnie dogodne i przejrzyste do analizy maszyn trójfazowych, można równania obwodowe zapisać w postaci

d¥f

(6.67)

«s = ^Ri‘_s+-^-+)<*>k'l's

dV_r

u_r = R_ri_r+—+j(to_t-®)?'_r

Cu

Równania (6.67) są zapisane we wspólnym układzie współrzędnych wirującym z prędkos-

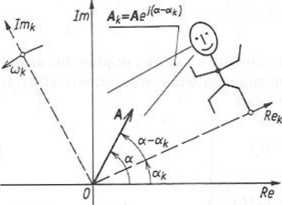
Rys. 6.31. Prądy i napięcia w trójfazowych    Rys. 6.32. Zapis wektora A w wirującym z prędkością to_k

uzwojeniach silnika indukcyjnego    układzie współrzędnych cią kątową <x>_k, którą dobiera się tak, by uzyskać najdogodniejszy zapis. Z prędkością 0)_k porusza się obserwator opisujący rozpatrywaną wielkość A tak, jak to pokazano na rys. 6.32. Pomijając wpływ nasycenia oraz straty w żelazie, można wprowadzić wektory przestrzenne strumieni

(6.68)

CHARAKTERYSTYKI SILNIKÓW ZASILANYCH Z SIECI SZTYWNEJ

491

UVW

V, = LJ, + L„i_r

<P_r = L_ri_r + L_mi_s

przy czym: L_s, L_r—indukcyjności własne stojana i wirnika, zmierzone przy symetrycznym trójfazowym zasilaniu uzwojeń; L_m — wypadkowa indukcyjność wzajemna między uzwojeniami stojana i wirnika.

W stosunku do wartości indukcyjności fazowych zachodzi następująca relacja:

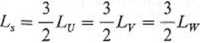
Jest ona ważna również dla indukcyjności wirnika oraz indukcyjności wzajemnych. Równanie momentu rozwijanego przez silnik ma postać

^Me = -jP lm(V* ■ g = jpL_m Im (i, • i*)    (6.69)

T*o wprowadzeniu współczynników rozproszenia

L    L    1²    1

<r_s = —;    (y =    a = 1--— = 1 -

K    Lj    L,L_r    (l + <g(l+<7,)

równanie momentu można przedstawić jako

- Im(!P_s ■ V?)    (6.70)

3 aL_m

Przy czym Im oznacza urojoną składową iloczynu w nawiasie, a gwiazdka (*)—sprzężoną wielkość wektorową.

(6.71)

W symetrycznym układzie trójfazowym wektory przestrzenne są określone relacjami = u_L.-t-au_K + a² Uyy i_s = i_v + a i_v +a² i_w ^ur = u_u + a«„ + a² u_w i_r = i„+at„+a² i„