ALG'7

277

11.6. Rozwiązywanie układów równań liniowych metodą Gaussa

co pozwoli na zapisanie całości w postaci macierzowej:

^r5 0 1 Yjt> /V

1 1 -1 y = 6 .

,2 -i 1 JUJ k

Wymnożenie tych macierzy powinno spowodować powrót do klasycznej, czytelnej postaci.

Zaletą reprezentacji macierzowej jest możliwość zapisania wszystkich współczynników liczbowych w jednej tablicy Nx(N~l) i operowania nimi podczas rozwiązywania układu. Operacje na tej macierzy będą odbiciem przekształceń dokonywanych na równaniach (np. w celu eliminacji zmiennych, dodawania równań stronami...).

Z uwagi na łatwość implementacji programowej, bardzo szeroko rozpowszechnioną metodą rozwiązywania układów równań liniowych jest tzw. eliminacja Gaussa. Przebiega ona zasadniczo w dwóch etapach: sprowadzania macierzy układu do tzw. macierzy trójkątnej, wypełnionej zerami poniżej przekątnej, oraz redukcji wstecznej, mającej na celu wyliczanie wartości poszukiwanych zmiennych. W pierwszym etapie eliminujemy zmiennąx z wszystkich oprócz pierwszego wiersza (poprzez klasyczne dodawanie wiersza bieżącego, pomnożonego przez współczynnik, który spowoduje eliminację). W etapie drugim postępujemy identycznie ze zmienną v i wierszem 2, w celu ostatecznego otrzymania macierzy trójkątnej. Popatrzmy na przykładzie:

• eliminacja¹ z wierszy 2 i J (efekt dodawania wierszy jest pokazany w etapie następnym):

5x+0y+lz=9

lx+ly-h=6 *(-0,4)

2x-ly+ lz-0 <■

• eliminacjay z wierszy I i 3 (w pierwszym nie ma już nic do zrobienia):

5x+0y+lz = 9

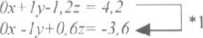
otrzymujemy ostatecznie macierz trójkątną.

5x+0y+lz = 9 0x+ ly-l,2z - 4.2 -0x+0y-0,6i =0.6