CCF20090120115

to, że mamy rozwiązać następujące zadanie: czemu jest równe y, jeżeli V    Oczywiście,

y = In x jest jakąś odpowiedzią. Odpowiedź kompletna 'będzie zależała od innego warunku; nie wystarczy bowiem wiedzieć, jak szybko ciało się porusza, trzeba jeszcze wiedzieć, gdzie się ono znajduje w określonym momencie.

RÓWNANIA RÓŻNICZKOWE

Bardzo wiele zagadnień praktycznych prowadzi do tzw. równań różniczkowych. Istotę równań różniczkowych najlepiej można poznać rozpatrując przykład.

Światło lampy elektrycznej rozchodzi się jednakowo we wszystkich kierunkach. Często — np. w reflektorze samochodowym — jest to niewygodne; wolelibyśmy, aby całe światło było skoncentrowane w jednym kierunku. Osiąga się to umieszczając za lampą zwierciadło. Jaki kształt powinno mieć 'zwierciadło, aby światło odbite tworzyło idealną wiązkę równoległą?

Wiadomo, jak zachowuje się światło, gdy pada na zwierciadło. Podkreślona duża litera V daje obraz tego zachowania. Odcinek poziomy wyobraża zwierciadło; lewe ramię litery V wyobraża światło padające na zwierciadło, a prawe ramię — światło odbite od zwierciadła. Oba ramiona litery V muszą tworzyć ze zwierciadłem te same kąty. W podobny sposób odbija się od bandy kula bilardowa, jeżeli nie jest wprawiona w ruch obrotowy.

Jeżeli za lampą umieścimy zwykłe zwierciadło płaskie, to nie otrzymamy wiązki dokładnie równoległej. Światło odbite będzie rozpraszane w 'różnych kierunkach, co można zobaczyć sporządzając rysunek.

Moglibyśmy zabrać się do naszego zadania biorąc dużą liczbę małych kawałków zwierciadła i próbując utworzyć z nich taki łańcuch, aby otrzymać wiązkę równoległą światła. Na ryc. 41 P jest punktem, w którym umieszczono lampę elektryczną. O jest jakimś innym punktem; chcemy otrzymać wiązkę światła biegnącą w kierunku OP. OA wyobraża mały kawałek zwierciadła umieszczony tak, że światło wychodząc z punktu P i padając na zwierciadło w punkcie O odbija się wzdłuż prostej OP. Oczywiście, światło wychodzące z punktu P i padające na zwierciadło pomiędzy punktami O i A zostanie odbite w kierunku odchylającym się nieco od prostej OP ku górze; jeżeli jednak odległość O A jest mała, to odchylenie to nie będzie znaczne.

D

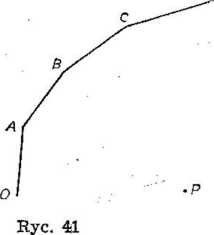
W punkcie A dołączamy następny kawałek zwierciadła, AB_t w taki sposób, aby promień świetlny PA został odbity we właściwym kierunku, tj. równolegle do ÓP. Podobnie, następny kawałek zwierciadła, BC, musimy tak obrócić, aby promień PB został odbity równolegle do OP. Proces ten kontynuujemy: każde zwierciadło umieszczamy tak, aby jego najniższy punkt stykał się z najwyższym punktem zwierciadła poprzedniego, a następnie tak je obracamy, aby odbijało światło we właściwym kierunku.

533