Cialkoskrypt"4

446 6. Zadania różne

a = VkRT = V 1,33 • 68,7 - 253 = 152,24 m /s,

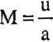
100

152,24

= 0,6569.

ZADANIE 6.13

Powietrze atmosferyczne o parametrach p₀ = 0,1 MPa, T₀ = 300 K rozprężając się wypływa do absolutnej próżni (przypadek idealny). Obliczyć prędkość wypływu, liczbę Macha, współczynnik prędkości X. Indywidualna stała gazowa R = 287 J/(kg-K).

Rozwiązanie

Korzystamy z równania energii w postaci

— +

2    k-1

a

2

o

K-1

Przy wypływie do próżni p = 0, T = 0, a = VtcR • T = 0. Uzyskana wówczas prędkość wypływu jest prędkością maksymalną:

=

K-1

Liczba Macha

—

K-1

kRT₀ -

—RT₀ = -287-300 =776,34 m/s. K-1    ⁰ V 0,4

U 776

^Mmax

a 0

Współczynnik prędkości (prędkość gazu jest odniesiona do krytycznej prędkości dźwięku)

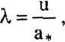
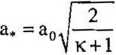
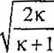
RT₀ =

J— 287-300 =316,94 m/s, y 2,4

X

max

776,34

316,94

= 2,45,

a*

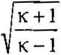
[1,4 + 1 V 1,4-1

Względna prędkość maksymalna u_max/a* zależy tylko od rodzaju gazu (jedno-, dwu- lub wieloatomowy).

ZADANIE 6.14

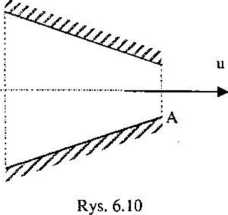
Powietrze atmosferyczne o parametrach p₀ = 0,1 MPa, T₀ = 300 K wpływa do obszaru o ciśnieniu p = 0,079 MPa przez szczelinę mającą kształt dyszy zbieżnej (rys. 6.10). Przekrój szczeliny A = 10~⁴ m² = 1 cm • 1 m. Obliczyć

strumień masy przepływającego powietrza. Przyjąć k = 1,4, indywidualną stałą gazową R = = 287 J/(kg-K).

Rozwiązanie

Prędkość wypływu wyznaczymy z równania energii dla przepływu izentropowego:

i + ~u² = i₀, i = c-T = — -RT,

2    °    ^p .    k-1

stąd

( -r \

1---

v ^To;

2k	K-1 * f P 1 ^K
--RT0	i- —
K-1	IpoJ

= 198,13 m/s,

u = ,/2(i„-i) = J^RTo

2-1,4

0,4

287-300

— = 0,75>

Po    Po

OA

1-0,79^1,4

K    1.4

p» j 2 _f 2    _

U + lJ ll4 + lj

0,5283.

Zatem przepływ gazu jest podkrytyczny.

Wyznaczmy taki strumień masy m , aby w przekroju wylotowym panowały parametry krytyczne, wtedy p = p«, p = p*, M = 1:

Pl

Po

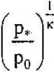
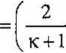
A P* m* = A • p* ■ u, = Ap0---	2k __	K-1 ~ 1 { l ^K
Po \j	K-1	IpoJ

p*	f ) 1	K—I	f \ 1	K-1 -	^2 )
Po	, K-1 xt2 1 +--M l 2 )		, ^K_1 ,2 l 2 )		U+iJ

i

K-]

oraz