Cialkoskrypt"7

452 6. Zadania różne

AS = M • (s₂ - Sj) = c_p • M ■ In — - MR In — =

452 6. Zadania różne

= — MRłn^-MRln-^f—ln^-~ln-^l =

K-l

Pil K-l T,

= 831₅f^ln ^{273 + 170}

^ 0,4    273 + 4

In — 1 = 8315 • 0,95028 = 7906,6---

0,2 J    kmol • K

= 3-282,2 = 846,6 J/K.

= 3 kg-7901,6

AS = mAs = 3 kg-7901,6 J/(kmol*K) = J

28 kg • K

ZADANIE 6.18

Wyznaczyć teoretyczną i maksymalną moc osiowej turbiny wiatrowej dla następujących danych. Na wysokości H [m] nad powierzchnią ziemi wieje wiatr z prędkością v_z [m/s]. Ma być wybudowana turbina wiatrowa o średnicy zewnętrznej wirnika D_z [m]; jej oś ma być usytuowana na wysokości H [m] nad poziomem ziemi. Na rysunku 6.12 pokazano hipotetyczny przepływ powietrza. Znane są parametry termodynamiczne powietrza, ciśnienie otoczenia p_ot [Pa] i temperatura t_ol [°c] na wysokości H [m], pozwalające

obliczyć gęstość p_ot [kg/m³] powietrza. Założyć, ze prędkość wiatru (przepływu powietrza) jest znana z pomiarów lub z aproksymacyjnej zależności

v = f(v_z,h).

Rozwiązanie

Przez przekrój turbiny wiatrowej o powierzchni A [m²] przepływa powietrze o gęstości p = p_ot z prędkością v [m/s]. Połę przekroju przepływowego wirnika turbiny (rys. 6.12):

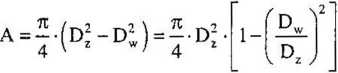
We wzorze tym D_z [m] i D_w [m] oznaczają odpowiednio zewnętrzną i wewnętrzną średnicę wirnika turbiny.

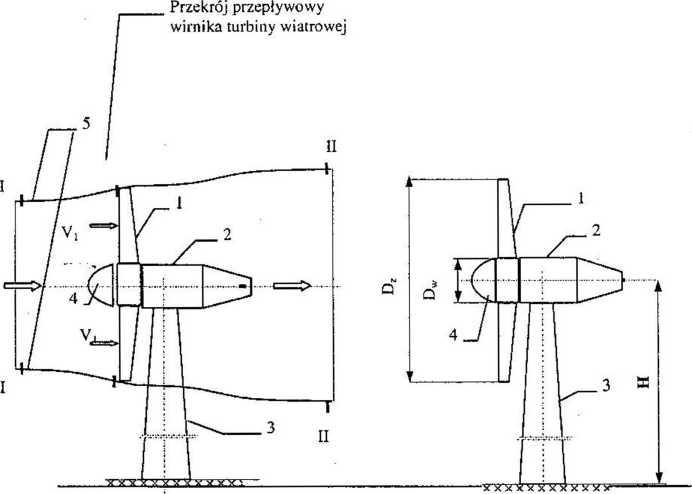
Rys, 6.12. Szkice pomocnicze do obliczeń turbiny wiatrowej; 1 - łopaty wirnika turbiny, 2 - generator energii elektrycznej, 3 - kolumna nośna, 4 - kołpak dopływowy turbiny, 5 - hipotetyczne linie prądu, I - przekrój dopływowy w górę przepływu, II - przekrój wypływowy w dół przepływu, Dz-średnica zewnętrzna wirnika Turbiny, D_w- średnica wewnętrzna wirnika turbiny

Poniższe wzory określają;

1)    strumień masy m [kg/s] powietrza przepływającego przez turbinę

rh = A ■ p • v ,

2)    strumień masy powietrza m, przepływającego przez przekrój 1-1 poprzedzający turbinę, w którym nie występuje oddziaływanie wirnika turbiny w górę przepływu

m, = A, -Pi -V,,

3)    strumień masy powietrza m^ przepływającego przez przekrój II - II za turbiną, w którym nie występuje oddziaływanie wirnika turbiny w dół przepływu

=A„ «p„ -V,,.

Można założyć, że gęstość powietrza w poszczególnych przekrojach przepływu jest taka sama, czyli