Elektronikawzad64

W. Ciążyński - ELEKTRONIKA W ZADANIACH

Ozęić 2: Analizi wpływu rmian tempera rury na pr*x układów półprzewodnikowych

Zadanie 2.13

■zas R

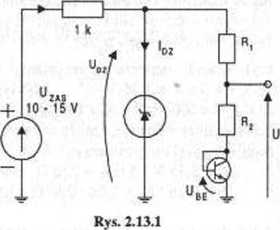
Dla przestawionego na rysunku 2.13.1 układu źródła napięcia odniesienia mamy w temperaturze T₀ = 25 °C następujące

dane:

-    napięcie zasilania zmieniające się w granicach 10-r 15 V

-    napięcie przebicia diody stabilizacyjnej wynosi Uoz= 6.2 V;

-    współczynnik wzmocnienia prądowego tranzystora wynosi fi = 50; prąd zerowy tranzystora Icbo = 5 nA;

-    spadek napięcia na złączu baza-einiter wynosi U be - 0,6 V;

-    rezystancje dynamiczne diody stabilizacyjnej i złącza baza-emiter można przyjąć jako równe zeru.

Przy wzroście temperatury- w zakresie do 75 °C można przyjąć, że:

-    współczynnik temperaturowy zmian napięcia diody stabilizacyjnej (Zenera) wynosi £dz= 1 mV / °C;

przyrost wzmocnienia prądowego wynosi Afi KfioAT) = 1 % / °C;

-    temperatura podwojenia prądu zerowego Icbo wynosi 7,5 °C;

-    współczynnik temperaturowy zmian napięcia baza-cmitcr tranzystora wynosi e*jr=-2,5 mV/°C;

Nałoży:

1.    obliczyć wartości jakie powinny mieć rezystancje R_t i R₂, aby wyjściowe napięcie odniesienia było w pełni skompensowane termicznie, oraz dla wybranych /?/ i R₂ obliczyć wartość napięcia odniesienia;

2.    przeanalizować jakie zmiany w rozwiązaniu wprowadziłaby konieczność uwzględnienia niezerowych rezystancji dynamicznych diody stabilizacyjnej (rpz) oraz złącza baza-emiter (r_flfc);

Rozwiązanie

Ad 1. Napięcie na diodzie stabilizacyjnej jest w obwodzie równoważone sumą spadku napięcia na złączu baza-emiter tranzystora, oraz spadków napięcia wywołanych przez prąd emitera tranzystora na dwu rezystorach R_t i R₂. Tak więc możemy napisać równanie „koła napięć”:

+    +    czyli prąd emitera:    /_g = ~!f .o**

"l ^+K2

Napięcie odniesienia równe sumie spadku napięcia na złączu baza-emiter tranzystora i rezystorze R2 wyniesie:

^    =U_K    -U„)    (2.13.1)

Rezystory Iii i R₂ musimy dobrać w sposób zapewniający kompensację zmian temperaturowych napięcia odniesienia. Do zależności (2.13.1) powrócimy po dokonaniu tego wyboru. Teraz zwróćmy tylko uwagę, że napięcie odniesienia nie zależy od napięcia zasilającego Uzas- Prąd zasilający I/as w rzeczywistym układzie musi tylko być większy od prądu emitera tranzystora (zależnego od wybranych R_t i R₂) o tyle, aby reszta płynąca przez diodę stabilizacyjną jako luz mogła zapewnić odpowiedni punkt pracy na jej charakterystyce w zakresie przebicia. Warunek h < Izas zostanie uwzględniony przy wyborze rezystorów R, i R₂.

R    n,

Hm—
r 1	y
1 [ J
- ,	* L!

Rys. 2.13.2

Rozwiązanie zilustrujemy za pomocą schematu zastępczego układu dla zmian temperatury przedstawionego na rysunku 2.13.2. Przyrost prądu emitera możemy obliczyć jako:

_A/    A U_l)Z-AU_SE

^£    & + R₂

czyli zmiana napięcia odniesienia wynosi:

AU*.    + R, Al_s = AU,_t: +—^-(AU_ra —AU_ef:)    (2.13.2)

J\| l XV 2

Równanie to jest oczywiście różnicową (przyrostową) postacią równania (2.13.1) i równie dobrze moglibyśmy nie wykorzystując schematu zastępczego otrzymać je różniczkując równanie (2.13.1). Aby AU min było równe zeru musi zachodzić:

^^u*^e>0=MJ°^z' ^{skąd mamy:}

AU,_cR,=-AU_mR₂ czyli    =    (2.13.3)

r₂ a u_be e_SE

Ponieważ s^jest zawsze ujemny z powyższego jasno wynika, że współczynnik temperaturowy diody stabilizacyjnej edz musi być dodatni. W naszym przypadku:

^R* ^lmV/“^c . _{= 040}    (2,13.4)

Teraz już z równania (2.13.1) można obliczyć wartość napięcia odniesienia:

(/ . =L' +--1-(U_n7 -U_pr)=0.6 V + ^{6,2 V}= 4,6V    (2.J3.5)

*^E (RJR₂) + V ^m **    0,40+1

czyli spadek napięcia na rezystancji R₂ wynikający z przepływu prądu l_t- wynosi 4,6 V - 0.6 V = 4,0 V.

Prąd płvnący ze źródła zasilania wynosi przynajmniej:

J^ov-M^v.3._gmA

R

1 kś2

Ta wartość wyznacza maksymalny możliwy do przyjęcia prąd emitera. Przyjmując na przykład prąd równy około połowy tej maksymalnej wartości, tzn. h: = 2 mA (wtedy nawet przy minimalnym napięciu zasilającym jeszcze 1.8 mA przepływa przez diodę stabilizacyjną, co powinno zapewnić jej właściwy punkt pracy) otrzymujemy:

R₂ = 4 V / 2 mA = 2 kO, oraz R, = 0,40 • R₂ = 0,40 • 2 kH = 800

Sprawdźmy jeszcze moce wydzielane w elementach w przypadku przyłożenia maksymalnego napięcia zasilającego.