Image67

132
mamy
jR = mg cosa.
Ponieważ kula porusza się bez poślizgu, punkt styku z równią pochyłą jest chwilowym punktem obrotu, zatem prędkość środka masy
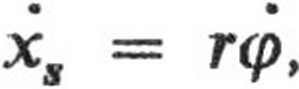
skąd, po zróżniczkowaniu, otrzymujemy wyrażenie na przyspieszenie środka masy
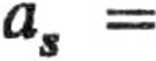
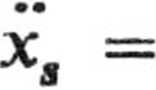
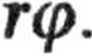
Podstawiając tę wartość do równań ruchu i rugując z nich T mamy
|
/ |
I\ |
• | ||
|
Im + |
r2)0* " |
= rng |
sina, | |
|
skąd |
mgr2 |
sina | ||
|
mr2 |
+ / |
• | ||
|
Dla kuli jednorodnej | ||||
|
2 2 |
• |
5 | ||
|
— _ mrz |
i |
= |
= - g sina. 7 w | |
|
Dla powłoki kulistej | ||||
|
h |
2 2 = 3™ |
• i |
as2 = |
3 . = - g sina. |
|
Stąd |
4 |
• | ||
|
asi ~ |
«.2 = |
35 9 |
sma. |
2.91
a.
mgr2 sina
a, — —7,-
mr2 + I
Dla kuli jednorodnej
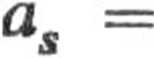
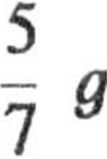
sina.
Dla walca jednorodnego
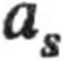
2 .
- g sina. 3 y
b. Przyspieszenia środków mas rozważanych ciał są stałe, jednostajnie przyspieszony. Szukaną prędkość wyznaczamy ze
zatem
wzoru
ruch jest
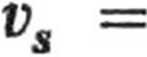
ast.
Biorąc pod uwagę, że
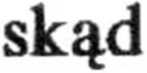
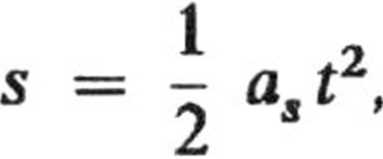
otrzymujemy
Dla kuli jednorodnej
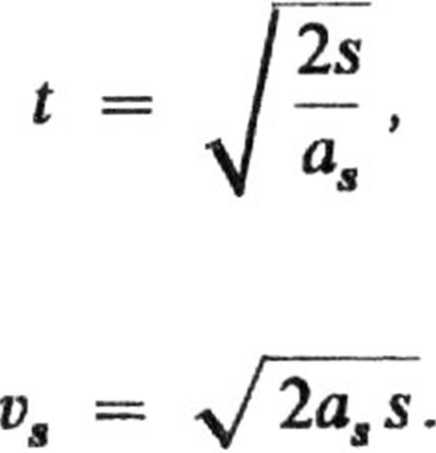
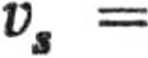
10
T
gs sina
Dla walca jednorodnego
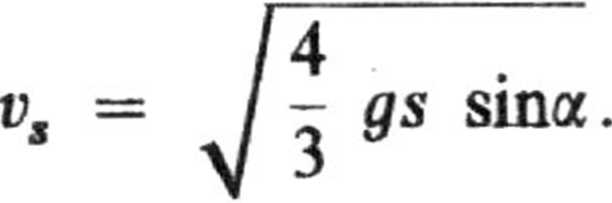
Wyszukiwarka
Podobne podstrony:
Image67 (7) 132 maj II R = mg cosa. Ponieważ kula porusza się bez poślizgu, punkt styku z równią poc
23 luty 07 (68) Ponieważ suwak 3 obraca się razem z jarzmem, to jego prędkość kątowa jest równa pręd
geolog lab23 Dolomity - skały utworzone z minerału dolomitu i zmiennych ilości kalcytu (Ca,Mg CO3).
DSC00064 (2) m a, którego sin« = —
ProgramProdukcjiSTAR25 lyj^A/ i g-j jr V , m mg, »« v,- P»- •- - «CT 3- « • V ł* •
geolog lab23 Dolomity - skały utworzone z minerału dolomitu i zmiennych ilości kalcytu (Ca,Mg CO3).
Mamy 75% odzyskanych należności ponieważ wiemy, że najważniejszy na tym etapie jest pierwszy kontakt
JJM polska Mamy 75% odzyskanych należności ponieważ wiemy, że najważniejszy na tym etapie jest pierw
DSC00258 (21) 132 Ponieważ pas ściskany belki pochylony jest pod kątem / do poziomu, to oprócz skład
DSC00263 (23) 132 Ponieważ pas ściskany belki pochylony jest pod kątem a do oprócz składowej poziome
Ciepło właściwe przy stałym ciśnieniu ZI zasady termodynamiki mamy dQ = dU + pdV Ponieważ U zależy t
schemat rownia pochyla RÓWNIA POCHYŁA N+R =0 jj - współczynnik tarcia (kinetycznego) N = mg• cosa =
mech2 70 *Y t*= -2,42 m X = X, X = -G ain a - P + P X = -mg sina - f mg cosa+ P, ~ m x = -mg sin a-
mech2 70 *Y t*= -2,42 m X = X, X = -G ain a - P + P X = -mg sina - f mg cosa+ P, ~ m x = -mg sin a-
132 RECENZJE, OMÓWIENIA. NOTY szawskiego”. Ponieważ znałem K. Pol-lacka jako „wszędobylskiego”
więcej podobnych podstron