img003 2

J4 W5t<p

jest macierzą wariancji i kowariancji. Wyznacznik _;'«£j nosi nazwę wariancji uogólnionej. Często rozkład ton oznacza się symbolem F).

Rozkład x^l {chi-kwadrat) o k stopniach swobody - rozkład zmiennej losowej ciągłej o funkcji gęstości prawdopodobieństwa określonej wzorem

/(/) =

2

(_Z-y*-Vł*^ł

dla y:²>0,

0    dla

Rozkład y² jest ściśle związany z rozkładem normalnym, jeżeli bowiem niezależne zmienne losowe C’, (i-l, 2, k) mają rozkład .VfO, I), to

t

£ U i =£“ ma rozkład y² o k stopniach swobody.

i-t

Rozkład t Studenta o k stopniach swobody - rozkład zmiennej losowej ciągłej o funkcji gęstości prawdopodobieństwa określonej wzorem

/0>=

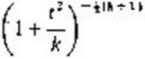
dla

— x <t< co .

Jest to dość częsty rozkład różnych statystyk. Jeżeli U ma rozkład #{0, 1), a V ma rozkład o k stopniach swobody i jeżeli zmienne U i V są nie-

U

zależne, to zmienna /= ___ma rozkład t Studenta o k stopniach swo-

\Vjk

body.

Rozkład F Snedecora o k_v i k₂ stopniach swobody - rozkład zmiennej losowej ciągłej o funkcji gęstości prawdopodobieństwa określonej wzorem

	riłlkt+k,))	pł«l~2)	dla F>Q,
f{F)=	r(ik,)r^k2)\kj |	kt \w,«,
		J *1V
	0		dla 0.

Jest to rozkład używany najczęściej w analizie wariancji. Jeżeli V, ma rozkład*² o kx stopniach swobody, a zmienna V* ma rozkład y² o k_z stopniach

swobody i jeżeli zmienne V_x i V₁ są niezależne, to zmienna

V, k >

F=—• —

y₂ k_t

ma rozkład F Snedecora o k₂ i k_z stopniach swobody.

Estymator — dowolna statystyka Z służąca do oszacowania nieznanej wartości parametru 0 populacji generalnej.

Rozkład estymatora — rozkład prawdopodobieństwa statystyki będącej estymatorem parametru 6.

Parametry rozkładu estymatora — najważniejsze to wartość oczekiwana E(Z) oraz wariancja D²(Z) w rozkładzie statystyki Z będącej estymatorem jakiegoś parametru 0 populacji.

Błąd przeciętny szacunku - pierwiastek z wariancji, tzn. odchylenie standardowe D(Z) w rozkładzie estymatora Z, za pomocą którego szacuje się parametr 0 populacji generalnej.

Estymacja punktowa — metoda szacunku nieznanego parametru 9 populacji, polegająca na tym_T że jako wartość parametru $ przyjmuje się wartość estymatora Z tego parametru, otrzymaną z danej, «-elementowej próby losowej.

Estymator nieobciążony — estymator Z spełniający równość E{Z)=B, oznaczającą, że estymator Z szacuje parametr 0 bez błędu systematycznego.

Estymator efektywny — estymator Z o możliwie małej wariancji D\Z). Stosowanie estymatora efektywnego oznacza popełnianie małego błędu przeciętnego szacunku D{Z).

Estymator zgodny - estymator Z parametru 6 spełniający warunek lim P{\z„-9\ <e}= I. t2n. estymator, który jest stochastycznie zbieżny

do parametru 9, C2yłi jest to estymator podlegający działaniu prawa wieł-.., kich liczb. Gdy używa się estymatora zgodnego parametru &, to stosowanie większych prób poprawia dokładność szacunku tego parametru.

Estymator wystarczający {dostateczny) — estymator Z skupiający w sobie wszystkie informacje o parametrze 9 zawarte w próbie losowej.