Kolendowicz 7

■ Metoda ta umożliwia rozwiązanie wielu innych zagadnień: mogą być dane momenty /, i li oraz kierunki osi głównych 1 i 2, natomiast należy wyznaczyć momenty I_x, l_y i D_xy względem układu osi x i y obróconego o kąt a wokół początku układu 1,2. Podobnie jak poprzednio, wykreślamy układ osi prostopadłych I, D (rys. 5-31). Na osi poziomej odmierzamy odcinek O A odpowiadający I\ oraz odcinek OB odpowiadający I₂. Odcinek BA jest średnicą koła Mohra ze środkiem K. Aby wyznaczyć l_x i /,, prowadzimy średnicę DC tworzącą z osią poziomą kąt 2a. Z punktów C i D kreślimy odcinki pionowe CE i DF. Odcinki OE i OF przedstawiają momenty bezwładności I_x i l_y, a odcinek CE — moment dewiacji D_xy.

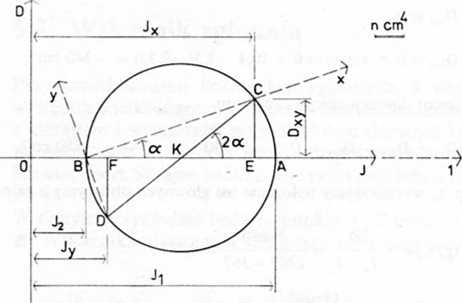
Rys. 5-31

■    Jeśli oś poziomą przyjmiemy równolegle do głównej osi bezwładności /, to kierunek osi x można wyznaczyć na rysunku przez obrót prostej wokół punktu B o kąt a. W tym przypadku kierunki obrotu kątów a i 2a są takie same.

■    Uzasadnienie konstrukcji koła Mohra jest bardzo proste. Konstrukcja ta jest przedstawieniem geometrycznym wyrażeń opisanych wzorami (5-27), (5-28) i (5-29).

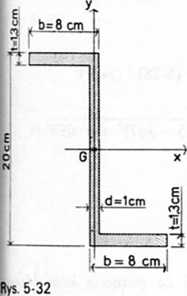
Przykład 5-9. Obliczyć momenty I_x. I_y i D_xy oraz znaleźć główne osie i główne momenty bezwładności metodą rachunkową i za pomocą kola Mohra dla zetownika przedstawionego na rys. 5-32 z osiami x i y przechodzącymi przez środek ciężkości przekroju.

Rozwiązanie

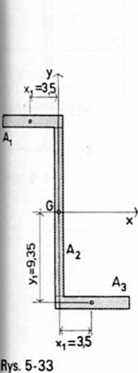
Pole przekroju dzielimy na trzy prostokąty i wyznaczamy środki ciężkości i ich współrzędne (rys. 5-33). Powierzchnie poszczególnych pól wynoszą:

A i = 10,4 cm²; A₂ = 17,4 cm²; A_} = 10,4 cm².

■    Momenty bezwładności pól częściowych względem osi x obliczymy korzystając ze wzoru (5-17):

bt³ ,    20-1,3³

'u = '₃* = -^ + ^ = —ij— + 10.4-9,35² = 913 cm⁴,

,    d(h-2t)³    1(20 — 2-1,3)³    _    ₄

hx =-j2-=-j2-= ^{439 cm} •

Momenty bezwładności pól częściowych względem osi y:

,    , ^tb3 a 2    1,3 - 8³

= ^I3y=~rt + ^AiXi =

12

12

+ 10,4-3,5² = 183 cm“ = /,„,

,    (h-2t)d³    (20 — 2-1,3)1³ _{1C 4}

l_2y =---=-77-= 1,5 cm

12

12

7 Mechanika budowli

97