lastscan12

W celu rozwiązania tego problemu zdyskontujemy kwotę 1000 zł na dzień wcześniejszy o I rok oraz o 3/4 roku. Obliczenia wykonujemy według wzoru (1.25). zatem wpłata wniesiona 1 stycznia powinna mieć wartość

a wpłata późniejsza o 3 miesiące musiałaby być większa i wynosić

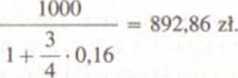
i

W pierwszym z powyższych przypadków dyskonto wynosi 137,93 zł. w drugim 107,14 zł i - co pozostawiamy do sprawdzenia Czytelnikowi - jest równe, odpowiednio, rocznym odsetkom od kapitału 862,07 zł i 9-miesięcznym odsetkom od kapitału 892,86 zł obliczonym przy stopie r = 16%.

■

Przykład 1.14

W dniu 1 stycznia 2001 r. kapitał ma wartość 1000 zł. Przy oprocentowaniu prostym danym stopą r = 25% ten kapitał po upływie roku, czyli 1 stycznia 2002 r., osiągnie wartość

1000(1+0,25) = 1250 zł. a rok wcześniej, czyli 1 stycznia 2000 r.. miał wartość

1000(1+0,25)-' = 800 zł.

Obliczając 2-letnie odsetki proste dla kapitału 800 zł z 1 stycznia 2000 r.. otrzymujemy

800(1 + 2 0,25) = 1200 zł.

Z kolei, poprzez 2-letnie dyskontowanie proste kapitału 1250 zł z 1 stycznia 2002 r. otrzymujemy

1250(1+2-0,25)-' = 833,33 zł.

Powyższe obliczenia ilustruje rysunek 1.3, na którym strzałki skierowane w prawo

I stycznia 2000 r.

1 stycznia 2001 r.

1 stycznia 2002 r.

800 zł <-

1000 zł

■> 1250 zł

800 zł

> 1200 zł

1250 zł

833.33 zł <■

Rysunek 1.3. Oprocentowanie proste i dyskontowanie (rzeczywiste) pnwtc

wskazują na wynik operacji oprocentowania prostego, a w lewo - dyskontowania prostego.

Przyczyna zaistniałej rozbieżności pomiędzy pierwszym wariantem obliczeń a dwoma następnymi będzie dla Czytelnika w pełni zrozumiała po zapoznaniu się z modelem oprocentowania składanego przedstawionym w rozdziale 3. W tym miejscu stwierdzimy jedynie, że w wariancie pierwszym mamy do czynienia ze złożeniem dwóch operacji: rocznego oprocentowania i rocznego dyskontowania, w związku z czym kapitał 1250 zł jest wynikiem 2-letniego oprocentowania składanego kapitału 800 zł. a tym samym - kapitał 800 zł jest wynikiem 2-letniego dyskontowania składanego kapitału 1250 zł. W dwóch pozostałych wariantach nie występowało składanie operacji rocznego oprocentowania ani dyskontowania i dlatego otrzymaliśmy inne wyniki niż poprzednio.

■

W rozdziale 4, przedstawiając zasadę równoważności kapitałów i związane z nią procedury obliczeniowe aktualizacji wartości kapitału, ponownie będziemy wskazywać na problemy interpretacyjne występujące przy korzystaniu z rachunku oprocentowania prostego.

1.8. Zadania

Uwaga: jeśli w zadaniu nie ustalono typu rachunku czasu, należy zastosować czas bankowy.

1.1.    Odsetki od 2-letniej lokaty o stałym oprocentowaniu są naliczane po terminie. Pani X. która wpłaciła na lokatę 2300 zł, odebrała przy jej likwidacji 3047,50 zł. Obliczyć roczną stopę oprocentowania lokaty.

1.2.    Przy jakiej rocznej stopie oprocentowania prostego wartość 2-letniej lokaty z odsetkami naliczanymi po terminie zwiększy się:

a)    o 15%,

b)    1,5-krotnie,

c)    przynajmniej dwukrotnie?

1.3.    Przedsiębiorca otrzymał półroczną pożyczkę w kwocie 15 000 zł. zobowiązując się spłacać co miesiąc bieżące odsetki naliczane przy rocznej stopie 18% i zwrócić pożyczkę na koniec roku. Obliczyć wysokość rat spłacanych na koniec kolejnych

1.4. Pożyczka 2700 zł otrzymana na początku roku będzie spłacona w 3 ratach na koniec lipca, listopada i grudnia. W każdej racie będzie spłacona 1/3 początkowej kwoty pożyczki oraz bieżące odsetki proste obliczane przy miesięcznej stopie prostego przy rocznej stopie 12.5% wartość

33

-