lastscan32

n, wówczas stopę oprocentowania rocznego r obliczamy, co można łatwo sprawdzić, według wzoru

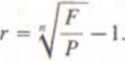
(3.3)

Gdy natomiast znamy wartości P, F oraz stopę r, wtedy do obliczenia czasu oprocentowania n korzystamy z wzoru

(3.4)

In (F/P) ln(l +r)

przy czym, jeśli obliczona w ten sposób wartość n nie spełnia warunku n e N, to nic istnieje taki czas, po którym w omawianym modelu oprocentowania rocznego kapitał P zwiększyłby swą wartość do F.

Przykład 3.3

Na początku sierpnia 2002 r. w prasie ukazała się informacja o kolejnej emisji dwuletnich obligacji skarbowych o oprocentowaniu stałym, w której napisano: ..kupujesz za 100 zł, otrzymujesz 116,42 zł (7,9% w skali roku)”.

Bez trudu zauważamy, że dwuletnie odsetki od tych obligacji nie są odsetkami prostymi, ponieważ wtedy roczna stopa byłaby większa od podanej stopy 7,9% i zgodnie z wzorem (1.6) wynosiłaby

16,42

100-2

8,21%.

Jeśli są to dwuletnie odsetki kapitalizowane po każdym roku. to stopę należy obliczyć według wzoru (3.3), a wynik

116,42

100

-1

= 7,90%

potwierdza to przypuszczenie. Na podstawie wzoru (3.1) możemy sprawdzić, że po upływie 2 lat nabywca obligacji otrzyma kwotę taką, jaką podano w informacji prasowej, czyli

F = 100-1,0790^: = 116,42 zł.

Przykład 3.4

Po ilu latach oprocentowania składanego przy rocznej stopie r = 15% kapitał P = 2500 zł wygeneruje odsetki / = 3500 zł?

Liczbę n możemy obliczyć bezpośrednio z wzoru (3.4) lub rozwiązując względem n równanie (3.1), czyli

6000 - 2500- 1,15".

i czego wyniku, że n - In2.4/In 1.15. Otrzymana wartc^d n jest liczbą niewymierną iw przybliżeniu równą 6.24), zatem przy kapitalizacji rocznej i stopie 15% nic Istnieje taki czas oprocentowania, po którym wartość kapitału wzrośnie dokładnie H\ 6000 zł. Bez trudu można sprawdzić, że po 6 latach wartość kapitału wyniesie 1*782.65 zł. a po 7 latach 6650.05 zł.

■

W praktyce zachodzi niekiedy potrzeba określenia czasu, po którym kapitał woi swą wartość. W takiej sytuacji według wzoru (3.4) obliczamy

(3.5)

ln 2

n =

ln(l + r)'

ipśli jednak wystarczy nam poznanie przybliżonej wartości n, to możemy skorzystać A tzw. reguły 70.

Reguła 70

rocznej stopie r (z domyślnym mianem %) i przy rocznym okresie ńtalizacji kapitał podwaja swą wartość w czasie n równym około 70!r lat.

Przykład 3.5

¹ Obliczymy w sposób dokładny i przybliżony, po ilu latach oprocentowania tego przy stopie r = 15% kapitał podwoi swą wartość.

Czas n, obliczony w sposób dokładny według wzoru (3.5), jest liczbą /ymiemą. po zaokrągleniu równą 4.96, co prowadzi do wniosku, żc po fwie 5 lal wartość kapitału zwiększy się ponad 2-krotnie. Zastosowanie luły 70 daje wynik

70

" = U = 4.67.

który leż oznacza, że wartość kapitału podwoi się po ok. 5 łatach. Jak widać, w obu wypadkach otrzymaliśmy bardzo podobny wniosek dotyczący czasu podwojenia tości kapitału, ale obliczenia według reguły 70 wykonaliśmy znacznie szybciej i bez użycia komputera czy kalkulatora.

Oprócz reguły 70 w podręcznikach matematyki finansowej można znaleźć także inne reguły obliczania przybliżonego czasu podwojenia wartości kapitału, np. regułę 72 czy regułę 69. Każda z tych reguł umożliwia bardziej lub mniej dokładne przybliżenie czasu podwojenia wartości kapitału w zależności od wysokości stopy r. W tabeli 3.4 podane są wartości czasu potrzebnego na podwojenie wartości kapitału przy różnych stopach rocznych, obliczone według wzoru (3.5) oraz według reguły 70. Jak widać, reguła 70 zawyża czas podwojenia wartości kapitału tylko przy bardzo niskich stopach, a już przy stopach wyższych od 2% - zaniża.

73