Matematyka 2 A7

416 V| Elementy itutystyki matemntycsitej

4. ESTYMATORY PUNKTOWE.

POJĘCIE ESTYMATORA. Zakładamy, że cecha X ma rozkład pr-stwa o CIP Hub funkcji pr-stwa p() lub dystrybuancic F. kiórc zależą od parametru 0. Postać tych funkcji jest nam znana, nie znamy natomiast wartości parametru 0. wiadomo nam tylko, że jest ona elementem danego zbioru O zwanego przestrzenią parametru. Przy tych założeniach poszukiwanie rozkładu pr-stwa cechy X sprowadza się do szacowania wartości parametru 0 .

Estymacją nazywa sic formę wnioskowania statystycznego polegającą na szacowaniu nieznanej wartości parametru 0 rozkładu pr-stwa cechy X nu podstawie próbki tej cechy. Rozróżnia sią estymację punktową i estymację przcd/ialuwą. Rezultatem pierwszej jest liczba, czyli punkt na osi liczbowej; wynikiem drugiej - przedział liczbowy.

Estymatorem parametru 0 nazywa się statystykę 0_n

ilct

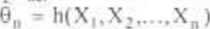
o wartościach z przestrzeni parametru 0, której wartość h(x_t,X2.....x_n)

dla zaobserwowanej próbki (x,.x₂.....x_n) przyjmuje się za wartość pa

ru mętni 0:

(4.1)

h(x„x₂.....x„ )«()

I icz.bę h(x,.x_:... ,x_n) w tej przybliżonej równości nazywa się oszacowaniem lub oceną parametru 0.

Podobnie określa się estymator (danej) funkcji g parametru 0

- jest to statystyka, której wartość dla zaobserwowanej próbki przyjmuje się za wartość g(0) funkcji g w punkcie 0

JAKOŚĆ ESTYMATORA Definicja estymatora dopuszcza istnienie wiele estymatorów' tego samego parametru I) Jest oczyw iste, że

różne estymatory parametru 0, nawet dla tej samej próbki (x,.x_:.....x_n )

dostarczają rożnych jego oszacowań. Powstaje wobec tego problem sensownego wy boru jednego lub kilku z nich. Racjonalność takiego wyboru osiąga się przez narzucenie pewnych warunków, jakie winien spełniać dobry estymator Do warunków tych zaliczamy: nieobeiążoność, zgodność oraz efektywność. Omów imy przede wszystkim nieobeiążoność

I Wartość przeciętna estymatora winna być równa wartości cstymowanego parametru Ten postulat prowadzi do następnej definicji.

Estymator 0„ purameiru 6. którego wartość oczekiwana jest równa wartości estymowanego parametru.

(4.2)    H(0_n)=O, n = l,2,...

nazywa się estymatorem nicobdążonym parametru 0 lub estymatorem be/ błędu systematycznego Estymator dla którego E(0„ )vd) nazywa się estymatorem obciążonym parametru 0 Przy tym różnica

(4.3)    E(0_n)-O

nosi nazwę obciążenia lub błędu systematycznego estymatora

Różnica (4.3) zwykle zależy od liczności próby n Estymator 0„ spełniający warunek

(4.4)    lim |h(0_rt )-(J|=0. czyli limh(0_n)^O

n    n-*vr

nazywa się asymptotycznie nieobciążonym estymatorem paranietni 0

2.Estymator może być nicobciążony. a mimo to jego wartości mogą być bardzo odległe od wartości estymowanego parametru Zrozumiałe. ze z dwu nieobciążonych estymatorów lepszy jest ten. który ma mniejszy rozrzut swych wartości wokół 0. Najważniejszą miarą takiego rozrzutu jest wariancja estymatora Zatem: r dwu meahaążonuh estymu-(arów tego samego parametru lepszy je.:: ten. którego wariancja jest mniejsza. Rozważania te prowadzą do następującej definicji.

Mówimy, że nicobciążony estymator 0_n parametru 0 jesi efektywniejszy od meobeiążonego estymatora 0_ tego parametru, gdy VarO„ <VarO_t|. Powiemy, że nicobciążony estymator 0„ parametru U jest najefektywniejszy w danym zbiorze nieobciążonych estymatorów tego parametru, gdy jest efektywniejszy Od każdego estymatora z lego zbioru.

PRZYKł AD 4.1. Niech (X,.X_:.X,) będzie PLP cechy X. hstymujemy nieznaną wartość oczekiwana p tej cechy, p = EX. Spośród estymatorów: