Scan0012 3

RACHUNEK WEKTOROWY

- (byCz - bzCy) i + (bzCx - b_xc_z) j + (p_xc_y ~ b_yCx) k.

Obliczmy teraz i loczyn skalamy wektorów u i bxc.

Otrzymujemy

~a ■ ( b x ~c j - a_x(b_yc_z - bzC_y) + a_y(b_zc_x - b_xc_z) + a_z(b_xc_y - b_yc_x).

_^ —>

Analogicznie liczymy iloczyn wektorowy a x b :

(a_yb_:-a_zb_y)i + (a_zb_x-a_xb_z) j +■ (a_xb_y - a_yb_x) k .

i j k

a x b -

a_x Qy a_z b_x by b_z

oraz iloczyn skalamy wektorów c i a x b , który dalej przekształcamy

~c -\li X b \ - c_x(a_yb_z - a_zby•) c_yifl_zb_x - a_xb_z) + cAa_xb_y - a_yb_x) = - a_yb_zc_x - a_zb_yc_x + a_zb_xc_y - a_xb_zc_y + a_xb_yc_z - a_yb_xc_z -~^ax{b_yc_z - b_zCy) + a_y(J>_zc_x - b_xc_z) ~ Q_z(b_xc_y -b_yc_x).

Udowodniliśmy zatem pierwszą równość ~a - f b x ~c ^ - c • |JiT x b j.

Na koniec obliczamy iloczyn wektorowy c x a :

i j k Cx Cy C_Z a_x a_y a_z

c x a

- (c_ya_z - czdy•) i + (c_za_x - c_xu_z) j + (c_xa_y - c_ya_x) k .

oraz iloczyn skaiamy wektorów b i c x a , który następnie przekształcamy

b • (7 x ~a ) - b_x(c_ya_: - c_za_y) + b_y(c_za_x - c_xa_z) + b_z(c_xa_y - c_ya_x) =

- a_zb_xCy - a_yb_xc_z + a_xby-c_z - a_zb_yc_x + a_yb_zc_x - a_xb_zc_y --a_x(b_yc_:-b_zc_y) + a_y(b_zc_x -b_xc_z) + a_z(b_xc_y -b_yc_x)-'a-[ł)x7]. Udowodniliśmy wice prawdziwość całej zależności.

b) Obliczamy najpierw iloczyn wektorowy b x c

b X ~C = (byC_z - b_zCy) i + (b_zc_x - b_xc_z) j + (b_xc_y - b_yc_x) k . Następnie liczymy iloczyn wektorowy wektorów a i b xT

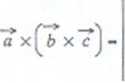
i	)	7
ox	Qy	oz

byc_z - b_zc_y b_zc_x - b_xc_z bxc_y - b_yc_x

Ąa_x{b_zcx - b_xcz) - Qy(b_yc_t _ _btCx]T Obliczymy teraz prawą stroną zależności, której słusz^ć " iloczyn skalamy a • c

«\dy{bxCy ~ byCx) - ^azib_:c_x _ b_xCg)] i + +[a_z(byC_z - b_zCy) ~ ^ax{b_xc_y - &_yCjc)] j +

mamy udowodnić - najpierw

a_xc_x + <

^a>^cy + a_tc_z.

Następnie mnożymy wektor b przez powyższą wartość Otrzymu' kt

^b ’0* ■~c)‘^a&xa_xcx + b_xa_vc    n"”

^x >^cy + b_xa_zcz) i +

+{b_ya_xcx + byayc_y + b_yQłCz)J ₊

Pozostaje do obliczenia iloczyn c • *J°**y*u_jemy 7-7 ._axbx j dalej    ^{7 7}

?■(■?•■?) = (<Wt,    _+CjaA)7 ₊

^+(c?a^x ⁺ V* c_?a₂6.)T.

Liczymy na koniec różnicą wektorów    -*\

.    ..    .    N^a*cJ-c-la.ft odejmując i

nrzekształcając wyrażenia stojące przy tyęh    '

•->->. -j .    ^Sa^ych wektorach jednostkowych

?. (7 • 7) - 7 ■ (7 • 7) - Mac, - ^    . _bxct)]7+

Udowodniliśmy zatem prawdziwość podanej zależności ^ ‘

4. Wyznacz gradient funkcji f (x,y,z) dla: a)Jtx,y,z) -Ab³ +y² +z³)

- BCc³ +y² + z²)‘^1/2 . gdzie A i B są stałymi.

Gradientem skalarnej funkcji i f(x.y,z) nazywamy w>u

i oznaczamy ten wektor symbolem grad/lub v/(ę: ^{0r 0} składowych 8f]dx, df/dy, dfldz gradientu wynika, że    ^ ^^Z'^A' ⁰P®^ra^orem nabla). Z definicji

wtf-% •' ⁺f7+#7

a) Obliczamy składowe wektora grad/    ^c~

f-^². #-Ky, |._Mz2.

Zatem zgodnie z definicją gradientu mamy

grad/ - 3Ar²T +2AyJ ...₂7