skanuj0094

5. Hównowłiął Junumi w rozctortc/onych roztworach wodnych

Ocena kompletności modelu matematycznego

Model matematyczny obejmuje 10 równań (13.7) - (13.16), w których występuje 10 niewiadomych: stężenia wszystkich składników roztworu (oprócz wody c_Hł0 ■ 55,34 mol/dnr) i rozpuszczalność c,. Wartości pozostałych wielkości pK,. p'K₃|, p^łK^. p'K^, p²Ka, pK_w podano w treści zadania. Model jest kompletny.

Rozwi ązani e

Należy obliczyć rozpuszczalność fosforanu(V) amonu i magnezu w wodzie, bez uwzględnienia protolizy jonów amonu i fosfornnu(V). W tym przypadku model matematyczny znacznie się upraszcza. W obliczeniach należy uwzględnić równanie (13.7) oraz równania bilansu materiałowego, przy czym:

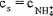
(13.17)

(13.18)

pomijamy. Podstawiając równania (13.13), (13.17) i (13.18) do równania (13.7) otrzymuje się:

(13-19)

K*-Cis'C**Ct“C«»

Iśtąd rozpuszczalność c, wynosi:

(1320)

Obliczenia

Po podstawieniu danych liczbowych otrzymuje się:

Po przeliczeniu stężenia molowego na stężenie wyrażone w g/100 cm³ roztworu rozpuszczalność soli MgNH*PO« wynosi:

_6,31-l<rM37_₈^ _[n_. _g

g

10

10

100 cm³ roztworu

CZĘŚĆ B

MODEL STECHIOMETRYCZNY

Do modelu stechiometiycznego podanego w części A zadania należy dodać reakcję dysocjacji soli dobrze rozpuszczalnej - fosforatiu(V) potasu:

KjPO^^+PO*¹-    (13.21)

Liczba składników roztworu zwiększyła się o jon potasu.

MODEL MATEMATYCZNY

W modelu matematycznym należy uwzględnić:

-    w bilansie materiałowym jonów POi³" dodatkowe źródło tych jonów w roztworze - sól KjPO*:

^C.^+C“V ^+<w ⁺V°J ^+cH^o.    03-22)

-    obecność jonów K* w roztworze przez ułpźenie bilansu materiałowego jonów potasu. Stężenie c_K, jest trzykrotnie większe niż formalne stężenie soli KjPO< (c), co wynika ze stechiometrii reakcji (13.21):

3c-c_k,    (13.23)

-    stężenie jonu potasu należy również wprowadzić do bilansu ładunków:

²V- ^+CNHI ⁺V %<>• “V- ^+2chfoi- ^+ch,po; ^+COH- <^l3M) Ocena kompletności modelu ₀

W skład modelu wchodzą równania (13.7) - (13.14), (13.22) - (13.24). Do modelu wprowadzono jedną niewiadomą c_K« i jedną daną - stężenie formalne K3PO4 - c. Liczba niewiadomych jest równa liczbie równań tworzących model. Model jest kompletny.

Rozwiązanie

Ponieważ podobnie jak w Części A przykładu w-treści zadania podano warunek, aby nie uwzględniać stężenia produktów protolizy jonów PO* j NHT, model matematyczny obejmuje jedynie równania: (13.7X (13.13), (13.17), (13.8), a równanie (13.22) upraszcza się do postaci:

^cs ^+c=ckp>-    (13-25)

Podstawiając równania (13.13), (13.17), (13.25) do wyrażenia na iloczyn rozpuszczalności (13.7) otrzymuje się: